Ab initio kinetic study of decomposition reactions of the unsym-dimethylhydrazine radical HNN(CH₃)₂

The combination of unsym-dimethylhydrazine (UDMH) and nitrogen tetroxide (NTO) is a widely adopted hypergolic bipropellant in liquid rocket propulsion systems, including spacecraft (e.g., launch vehicles and satellite propulsion systems) and missile technology^[1]. This mixture ignites spontaneously upon contact, requiring no ignition system. This unique combustion behavior makes the study of its fundamental combustion characteristics particularly critical. However, the high toxicity and corrosiveness of UDMH strongly hinder the related experimental investigations on its combustion characteristics. Although some kinetic models for hydrazine-based fuel/NTO systems have been developed and analyzed^[2−6] on the basis of previous theoretical calculations, the accuracy of the rate constants of elementary reactions still requires further refinement. Under this background, high-performance theoretical calculations using a quantum chemical method provide a safer alternative for understanding the chemical structure and the corresponding elementary reactions, which is of critical importance for understanding combustion characteristics and developing kinetic model.

To date, theoretical studies on hydrazine-based fuel/NTO bipropellant systems have primarily focused on thermal decomposition and H-abstraction reactions. Sun et al.^[7,8] conducted systematic theoretical investigations on methylhydrazine (MMH), examining both thermal decomposition and H-abstraction pathways. Their results demonstrated that H-abstraction from the terminal amine site, where it forms the trans-HNN(H)CH₃ radical, represents the predominant reaction channel among various possible abstraction routes. Tang et al.^[9] employed BMC-CCSD//B3LYP/6-311G(d,p) level of theory to calculate rate constants for H-abstraction reactions between UDMH and OH. Wang et al.^[10] and Kanno et al.^[11] independently investigated H-abstraction reactions involving the H atom, utilizing different theoretical approaches. Specifically, Wang et al.^[10] applied canonical variational transition state theory with small-curvature tunnelling correction (CVT/SCT) at the MCG3MPWPW91//MPW1K/6-311G(d,p) level, whereas Kanno et al.^[11] employed CBS-QB3//DSD-BLYP-D3(BJ)/def2-TZVP in combination with transition state theory (TST), respectively. These investigations consistently revealed that, similar to MMH, H-abstraction from the terminal amine site of UDMH is thermodynamically favored over abstraction from the methyl site.

Regarding the successive decomposition reactions of fuel radicals, Kanno et al.^[12] conducted computational studies on the reactions of NO₂ with three MMH-derived radicals (HNN(H)CH₃, H₂NNCH₃, and H₂NN(H)CH₂), using quantum chemical calculations and steady-state unimolecular master equation (ME) analysis based on Rice-Ramsperger-Kassel-Marcus (RRKM) theory. Their work yielded temperature- and pressure-dependent, product-specific rate coefficients for these reactions. The results demonstrated that the reactivity of these radicals with NO₂ depends strongly on both the heights of the roaming transition-state barriers between RNO₂ and RONO and the energy barriers for dissociation pathways. More recently, Bai et al.^[13] extended this investigation to examine not only the initial H-abstraction reactions but also the subsequent H-abstraction processes involving NO₂ and the primary radical product (HNNCH₃). Computational methods, including the CCSD(T)/CBS//M06-2X/6-311++G(d,p) single-reference approach and the MRCI(7e,6o)/CBS//M06-2X/6-311++G(d,p) multi-reference method, were adopted. Using the RRKM/ME approach, they obtained temperature- and pressure-dependent rate constants. These investigations revealed that these reactions play a crucial role in enhancing the overall combustion reactivity of the MMH/NO₂ system. It can be concluded that the successive decomposition reactions of fuel radicals in hydrazine-based fuels are of critical importance. However, existing theoretical calculations have primarily focused on MMH-derived radicals, with comparatively little research attention devoted to UDMH-derived radicals, despite UDMH's superior propellant characteristics, including its higher energy density. Furthermore, current studies have largely neglected other crucial decomposition pathways of these fuel radicals, such as isomerization reactions and β-scission reactions, which represent important decomposition mechanisms.

Prior computational studies^[14] have demonstrated that although H-abstraction reactions can generate two distinct fuel radicals, HNN(CH₃)₂ and H₂NN(CH₃)CH₂, the former represents the fuel-specific N-involved radical and is more preferentially formed. Consequently, this work systematically examines the decomposition pathways of HNN(CH₃)₂, including isomerization processes, β-scission reactions, and H-abstraction reactions with NO₂ and NO oxidizers. The study employs high-level quantum chemical methods to characterize the complete potential energy surfaces and obtain temperature-dependent rate constants for these elementary reactions. A comprehensive comparative analysis is subsequently conducted to elucidate the dominant reaction mechanisms and their relative importance across different temperature regimes, with particular emphasis on the similarities and differences relative to MMH.

In this paper, the structure optimizations and frequency calculations for UDMH and its products were performed using the M06-2X method^[15] combined with the def2-TZVP^[16] basis set. The zero-point energy correction factor is 0.971^[17], and the frequency correction factor is 0.984^[17]. The intrinsic reaction coordinate (IRC) approach was utilized to ensure the accuracy of the transition state structures and to derive the corresponding reactant and product geometries. The low-frequency torsional modes with wave numbers below 300 cm^-1 were identified as potential hindered rotors. For each identified torsional mode, a relaxed potential energy surface (PES) scan was performed by varying the corresponding dihedral angle in steps of 10° over a 360° range. All other geometric parameters were optimized at the M06-2X/def2-TZVP level of theory. Detailed results of electronic structure calculations are provided in the Supplementary File 1.

For high-precision single-point energy (SPE) calculations of stable molecules and transition states, coupled cluster methods combined with the cc-pVDZ and cc-pVTZ basis sets were used to obtain the energies, which were then extrapolated to the complete basis set energies using Eq. (1)^[18]. In the previous theoretical work on the unimolecular decomposition and H-abstraction reaction of UDMH^[14], the convergence of this level of theory was evaluated using larger basis sets (cc-pVQZ and cc-pVTZ). It was found that the calculated SPEs for the UDMH decomposition reactions at the CCSD(T)/CBS(T+Q) level were within 1 kcal/mol of those obtained at the CCSD(T)/CBS(D+T) level, indicating the feasibility of the originally chosen theoretical approach. As reported by Lee & Taylor^[19], T1 diagnostic values were defined as the Frobenius norm of the single substitution amplitudes vector of the closed-shell CCSD wave function divided by the square root of the number of correlated electrons to address size consistency, and the recommended upper limits of T1 diagnostic values are ≤ 0.025 for reactant species, ≤ 0.035 for product radicals, and ≤ 0.044 for transition states. As shown in Supplementary Table S1, all T1 diagnostic values in this study met these requirements, which demonstrates that the single-reference method can reliably describe the wave function. All quantum chemical calculations for geometry optimization, frequency analysis, and rotational potential scans were performed using the Gaussian 09 program^[20].

For the calculation of rate constants of reactions with tight transition state, such as the isomerization and β-scission reactions of HNN(CH₃)₂ radical, rate constants were determined using transition state theory (TST) based on the PES results. For the barrierless reactions of HNN(CH₃)₂ with NO₂ and NO, variational transition state theory (VTST) combined with the multi-reference method was applied. The CASPT2^[21] method with the cc-pVDZ basis set was used to calculate the minimum energy paths (MEPs) for the corresponding N-N bond dissociation processes in their products. An active space of (6e,5o) was selected^[22]. Based on the optimized geometries at CASPT2, the multi-reference configuration interaction method (MRCI) with the cc-pVDZ and cc-pVTZ basis sets is used to calculate higher-level single point energies, which are extrapolated to the CBS level using Eq. (2)^[23]:

Zero-point energy (ZPE) correction is included in the final energy of the optimized structures. Notably, the formation of pre- and post-reaction van der Waals complexes (i.e., reactant and product complexes) can influence reaction barriers and quantum tunneling effects. Therefore, it is common practice to account for them in rate constant calculations. In this work, phase space theory^[24] was utilized to estimate the microcanonical rate constants, where the potentials along the reaction coordinate were estimated by V = 10/R⁶, and the factor ten has the dimension of Bohr^6[25]. The RRKM theory combined with the ME method^[26] was employed to compute the pressure-dependent rate constants. The partition functions of reactants and transition states were approximated using the rigid rotor harmonic oscillator (RRHO) model. The low-frequency torsional mode treated as a one-dimensional (1D) hindered rotor^[27]. During rate constant calculation, the partition function of the identified hindered rotor mode replaced the original harmonic oscillator partition function and was subsequently used in the transition state theory calculations to obtain more accurate thermodynamic data and rate constants. Tunneling effects were accounted for using the 1D asymmetric Eckart model^[28] in the rate constant calculations. The collisional energy transfer model was treated using the empirical formula: <∆E>_down = 200(T/300)^0.85[13]. The Lennard-Jones parameters σ = 5.65 Å and ε = 258.55 cm⁻¹ were used for all intermediates^[13]. The bath gas Ar was used in the present study, and ε = 78.88 cm⁻¹ and σ = 3.47 Å were employed^[29]. In this work, the RRKM/ME simulations were performed using the MESS kinetic code^[30]. The pressure-dependent and high-pressure-limit (HPL) rate constants were fitted to a modified Arrhenius Eq. (3),

where, A, n, and E_a correspond to the pre-exponential factor, the temperature exponent, and the activation energy of the reaction, respectively. In addition, two-parameter fitting was adopted for reactions exhibiting non-Arrhenius behavior. The Arrhenius parameters of the relevant reactions of HNN(CH₃)₂ calculated in this work are provided in Table 1.

The influences of tunneling and hindered rotor treatments on the rate constants were comprehensively evaluated. As depicted in Supplementary Figs. S1–S4, the effect of tunneling on the calculated rate constants is minor at high temperatures, while the effect on R1 becomes significant at low temperatures. Moreover, the hindered rotor treatments also have little effect, except in the cases of R6 and R12. Additionally, the uncertainty analyses of the energy barrier and collisional parameter were performed on the calculated rate constants for the decomposition of UDMH radical. Supplementary Fig. S5 indicates that a variation of ± 1 kcal/mol in the energy barriers introduces only minor errors for reactions R1 to R4, particularly at high temperatures. In contrast, the error for R5 is relatively higher at 300 K. Generally, the uncertainties are more significant at lower temperatures than at higher ones. Regarding the collisional parameter, Supplementary Fig. S6 shows that the influence of σ on the rate constants is negligible. As depicted in Supplementary Fig. S7, additionally, a comparison of the rate constants with and without consideration of the vdW complexes revealed negligible effects for reactions R7, R8, R11, and R12, and differences for reactions R9 and R10 at low temperatures.

For the HNN(CH₃)₂ radical, the isomerization and β-scission reactions were investigated, with the PES results shown in Fig. 1. The H-migration isomerization reaction of HNN(CH₃)₂ (R1) has a relatively high energy barrier of 55.2 kcal/mol and the energy of the product H₂NN(CH₃)CH₂ radical is 12.0 kcal/mol higher than the reactant. This radical can undergo β-scission reactions with energy barriers of 36.2 kcal/mol and 41.3 kcal/mol, producing cis-HNNCH₃ (R2) and trans-HNNCH₃ (R3), respectively. This indicates that the β-N-C bond energies in HNN(CH₃)₂ are not uniform. Two β-scission channels were identified for the formed H₂NN(CH₃)CH₂: one corresponds to β-N-C bond dissociation, yielding H₂NNCH₂ and CH₃ (R4), whereas the other involves β-N-N bond dissociation, producing CH₂NCH₃ and NH₂ (R5). Their calculated energy barriers are 41.0 kcal/mol and 26.0 kcal/mol, respectively.

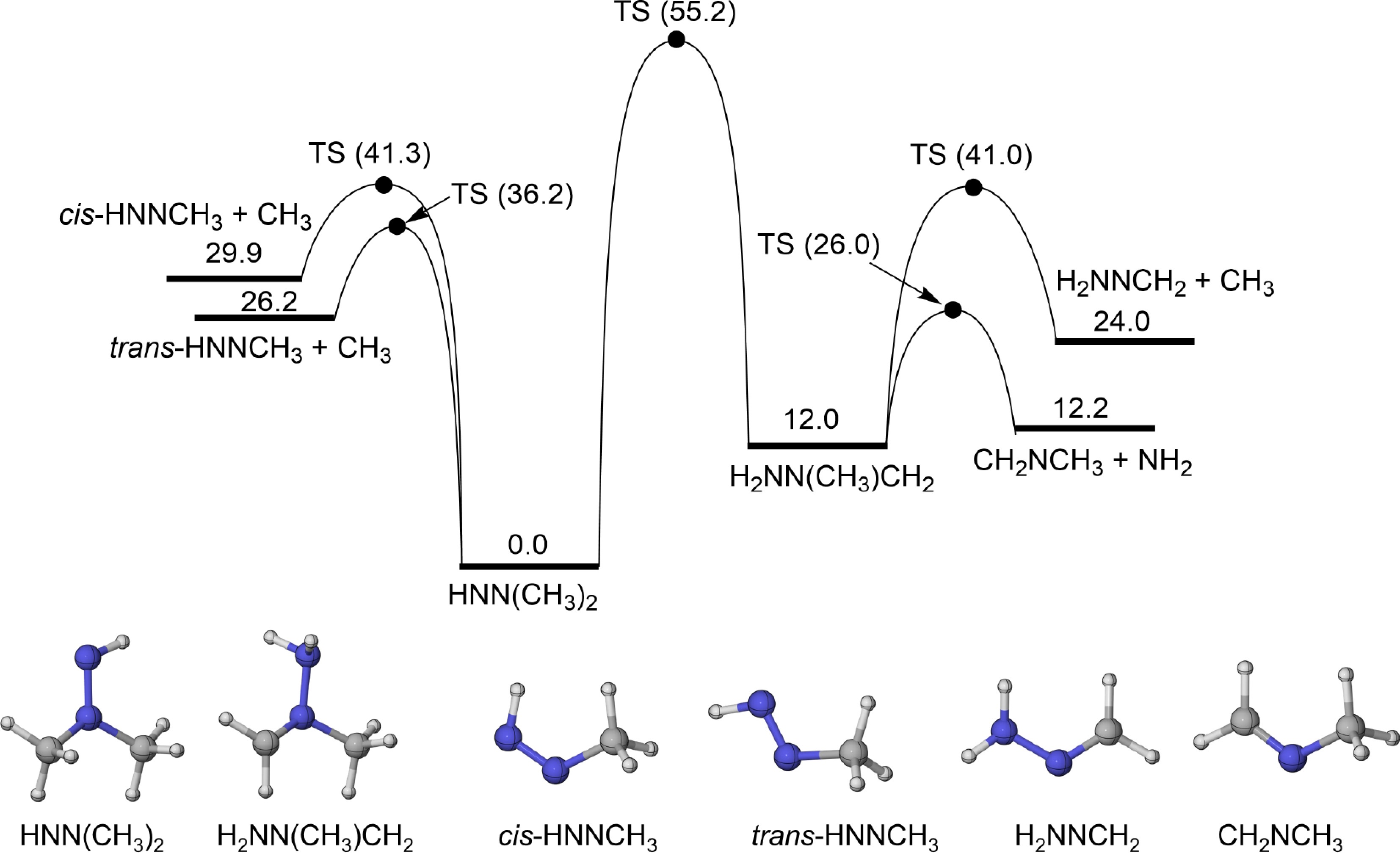
Figure 1. 

PES for the isomerization and β-scission reactions of HNN(CH₃)₂ radical at CCSD(T)/CBS(D+T)//M06-2X/def2-TZVP level (unit: kcal/mol).

To illustrate the effects of increasing the number of CH₃ groups (relative to MMH) on the decomposition trends of UDMH radicals, a comparison was carried out between the energy barriers of isomerization and β-scission reactions in UDMH radicals and those of MMH radicals with similar configurational characteristics (as shown in Fig. 2c−e). As shown in Table 2, the energy barrier for the isomerization reaction cis-HNN(H)CH₃ = H₂NN(H)CH₂ is lower than that of R1 by 5.9 kcal/mol. For β-N-C scission reactions that form CH₃ radical from the HNN(CH₃)₂ radical (R2 and R3), however, the calculated energy barriers are approximately 1 kcal/mol higher than those of trans-HNN(H)CH₃ and cis-HNN(H)CH₃. In addition, the energy barrier for the β-N-N scission reaction of the H₂NN(CH₃)CH₂ radical (R5) is comparable to that of the H₂NN(H)CH₂ radical. These similarities suggest that the β-scission reactions of UDMH radicals exhibit chemical properties comparable to those of MMH radicals.

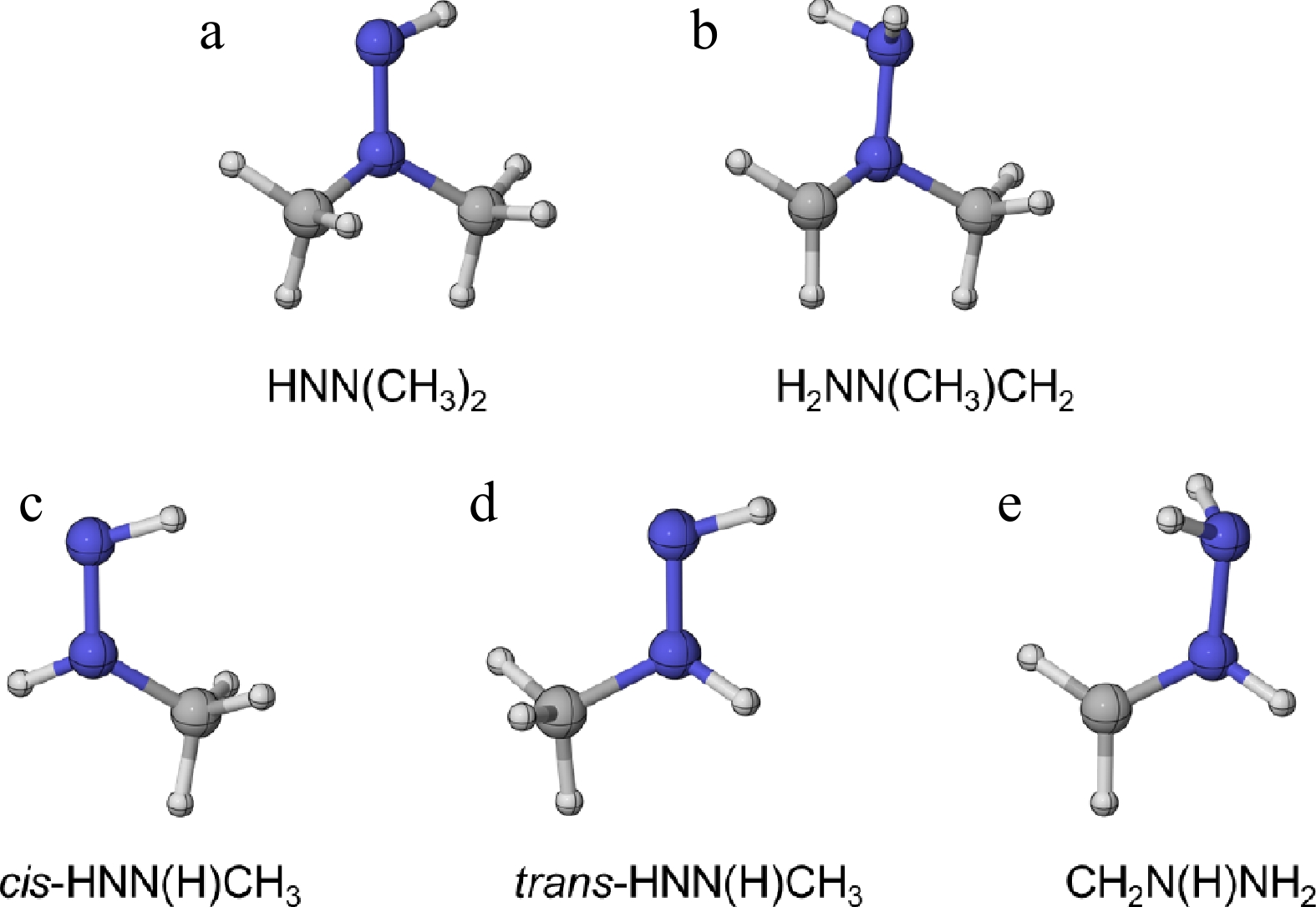
Figure 2. 

The optimized molecular configurations of (a), (b) UDMH radicals at the M06-2X/def2-TZVP level of theory, and (c)–(e) MMH radicals at the CASPT2/aug-cc-pVTZ level of theory^[31].

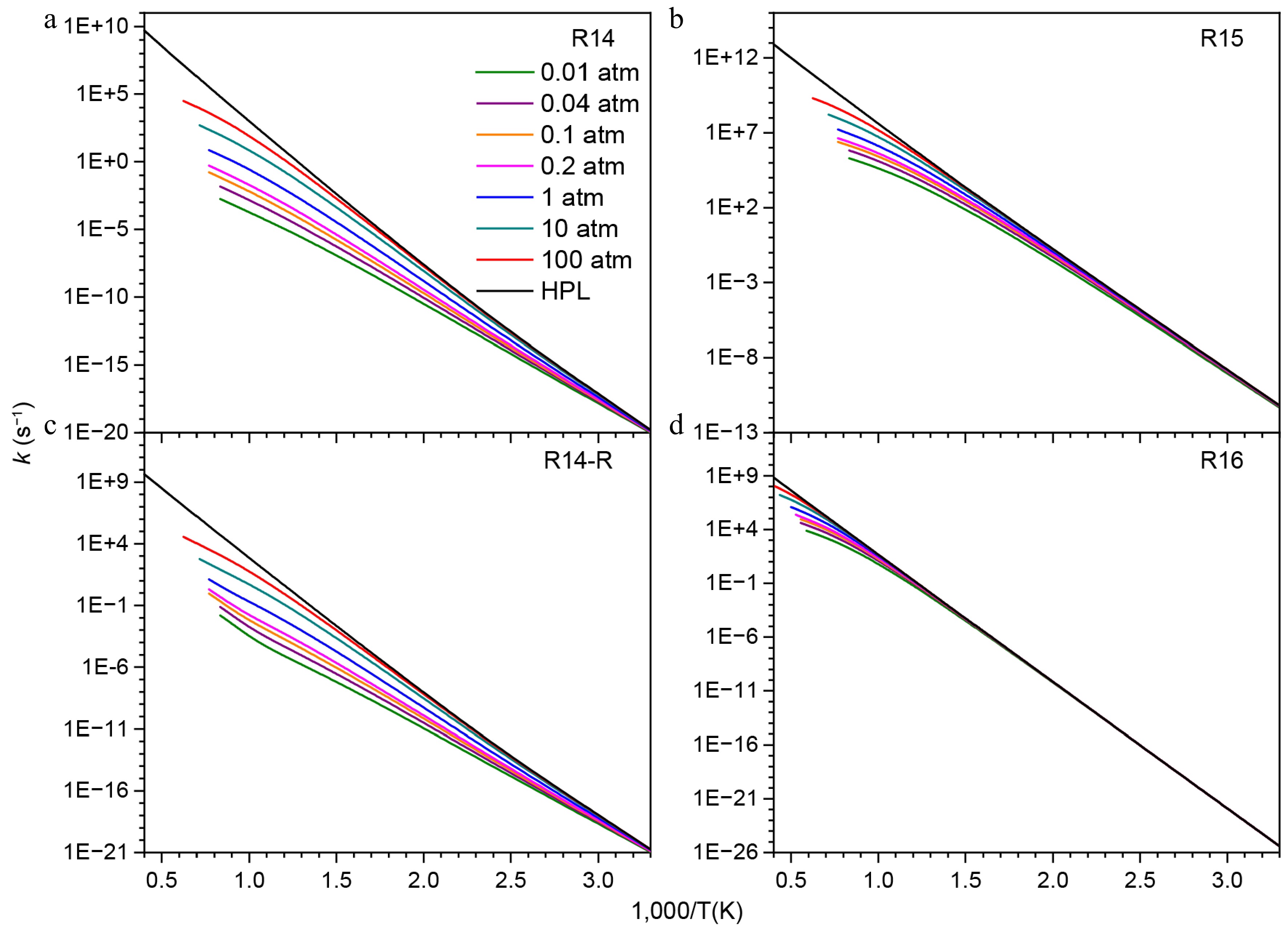
Figures 3 and 4 show the rate constants and branching ratios for the consumption pathways of HNN(CH₃)₂ and H₂NN(CH₃)CH₂ radicals, respectively. From Fig. 3a–c, it is noticeable that as the pressures increase, the rate constants of the reactions R1, R2, and R3 all represent increasing trends. By comparison, the H-migration isomerization reaction of HNN(CH₃)₂ radical (R1) exhibits a much lower rate constants than the other two β-scission reactions (R2 and R3), due to its much higher energy barrier. Similarly, consistent with the trend in transition energy barriers, Fig. 3d depicts that despite the branching ratio of R3 decreasing with temperature, it still contributes up to 75% of HNN(CH₃)₂ decomposition at a temperature of 2,500 K. In addition, the contribution of another β-scission reaction (R2) increases with temperature and reaches 25%, implying that HNN(CH₃)₂ radical is predominantly decomposed through β-scission reactions. As shown in Fig. 4a–c, the rate constants of R1-R (the reverse reaction of R1), R4, and R5 also increase as the pressure rises. Furthermore, the H₂NN(CH₃)CH₂ radical shows a higher rate constant and branching ratio (> 85%) for β-N-N scission reaction to produce CH₂NCH₃ and NH₂ (R5). This is attributed to its relatively low energy barrier.

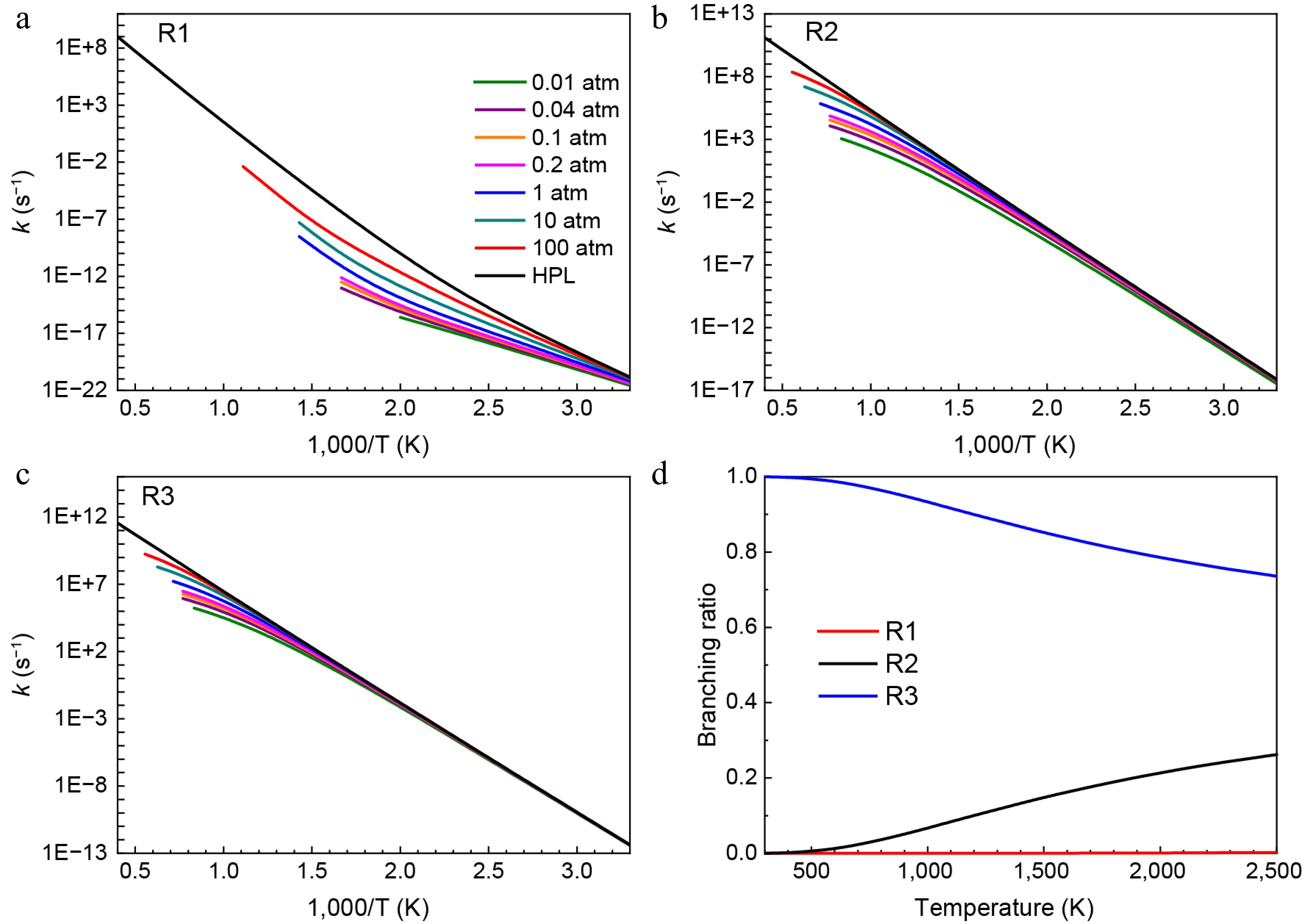
Figure 3. 

Pressure-dependent rate constants for (a) R1, (b) R2, and (c) R3. (d) Branching ratios of all consumption reactions of HNN(CH₃)₂ radical at HPL.

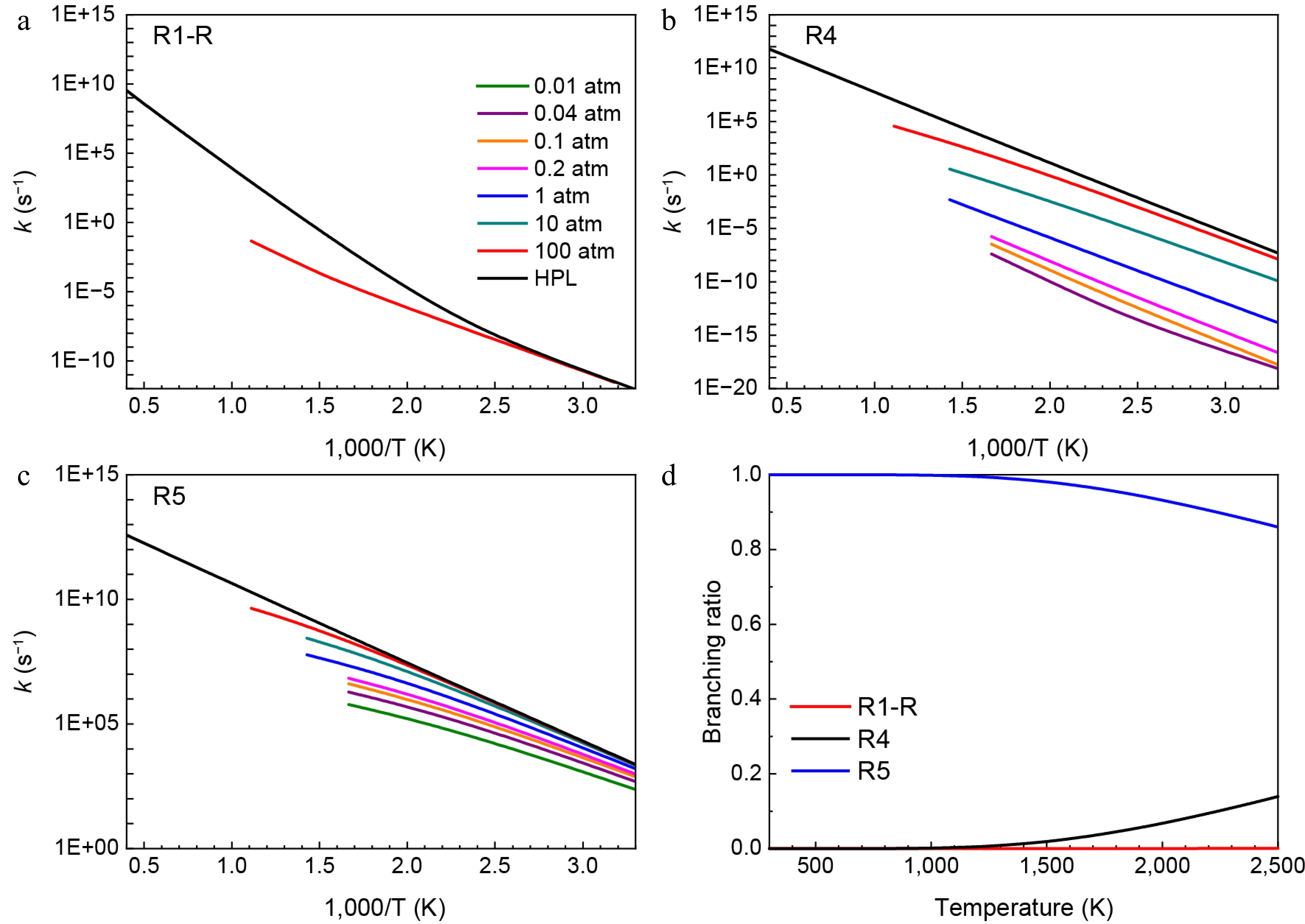
Figure 4. 

Pressure-dependent rate constants for (a) R1-R, (b) R4, and (c) R5. (d) Branching ratios of all consumption reactions of H₂NN(CH₃)CH₂ radical at HPL.

Sun et al.^[31] comprehensively investigated the isomerization and β-scission reactions of MMH radicals (H₂NNCH₃, trans-HNN(H)CH₃, cis-HNN(H)CH₃, and H₂NN(H)CH₂). They found that trans-HNN(H)CH₃ and its cis isomer cis-HNN(H)CH₃ exhibited distinct behavior in their decomposition. In addition, the β-scission of the NH₂ group in H₂NN(H)CH₂ to form methyleneimine is the principal channel for this radical's decomposition. Here, to gain further insight into the differences between the UDMH and MMH radicals, the rate constants for their β-scission reactions with similar configurational characteristics were compared. As shown in Fig. 5a, b, the β-N-C scission reactions forming CH₃ radicals from HNN(CH₃)₂ and HNN(H)CH₃ exhibit comparable rate constants. Specifically, the differences between the rate constants for R2 and the reaction trans-HNN(H)CH₃ = cis-HNNH + CH₃^[31] are within a factor of two at temperatures above 800 K. Moreover, R3 and its counterpart reaction, cis-HNN(H)CH₃ = trans-HNNH + CH₃^[31], show an even smaller difference in rate constants. This demonstrates that methyl substitution on the central nitrogen atom of the UDMH radical has a subtle influence on the kinetics of β-N-C scission reactions, suggesting that an analogous strategy may be applicable when developing kinetic models for UDMH combustion.

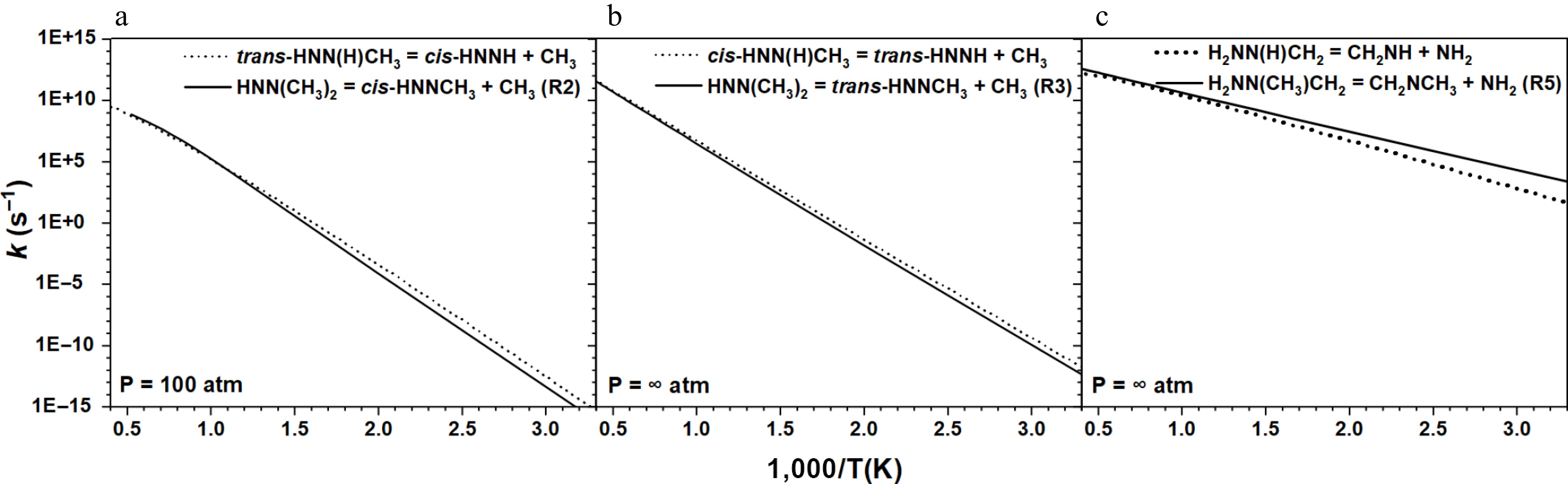
Figure 5. 

Comparison of the rate constants for the β-scission reactions of (a), (b) HNN(CH₃)₂, and (c) H₂NN(CH₃)CH₂ radicals with those of MMH radicals with similar configurational characteristics^[31].

For β-N-N scission reactions forming NH₂ radicals (Fig. 5c), the rate constants of R5 and H₂NN(H)CH₂ = CH₂NH + NH₂^[31] differ by approximately a factor of two within the temperature range of 800–2,500 K. However, this discrepancy increases significantly as the temperature decreases, reaching a factor of 63 at 300 K − a behavior distinct from that of β-N-C scission. This difference may arise from variations in the selected theoretical levels or inherent molecular properties. In summary, under the high-temperature conditions relevant to combustion, the kinetic properties of β-scission reactions in the UDMH radical are relatively similar to those of the MMH radical.

Addition-dissociation reactions of HNN(CH₃)₂ radical

NO₂ attacking

Considering the vital role of second H-abstraction reactions in the MMH/N₂O₄ combustion^[13], the H-abstraction reactions of HNN(CH₃)₂ with NO₂ and NO were investigated in this work. As depicted in Fig. 6a–c, the reaction of HNN(CH₃)₂ with NO₂ yields three stable configurations, i.e., cis-ONON(H)N(CH₃)₂, trans-ONON(H)N(CH₃)₂, and O₂NN(H)N(CH₃)₂. Table 3 shows that the formation of cis-ONON(H)N(CH₃)₂ and trans-ONON(H)N(CH₃)₂ releases 17.2 and 13.5 kcal/mol, respectively. In contrast, the analogous reaction NHN(H)CH₃ + NO₂ = trans-ONON(H)N(H)CH₃ release 17.99 kcal/mol^[12], which is higher than that of trans-ONON(H)N(CH₃)₂, despite their similar configurations. For N-N bond formation reactions, the energy released from HNN(CH₃)₂ + NO₂ (31.7 kcal/mol) is slightly lower than that from NHN(H)CH₃ + NO₂ (33.84 kcal/mol)^[12]. However, no stable transition state was found for the subsequent reactions of trans-ONON(H)N(CH₃)₂, differing from the reaction characteristics observed for NHN(H)CH₃ + NO₂^[12,13]. Consequently, the following PES analysis and rate constant calculations focus exclusively on the subsequent reactions of cis-ONON(H)N(CH₃)₂ and O₂NN(H)N(CH₃)₂.

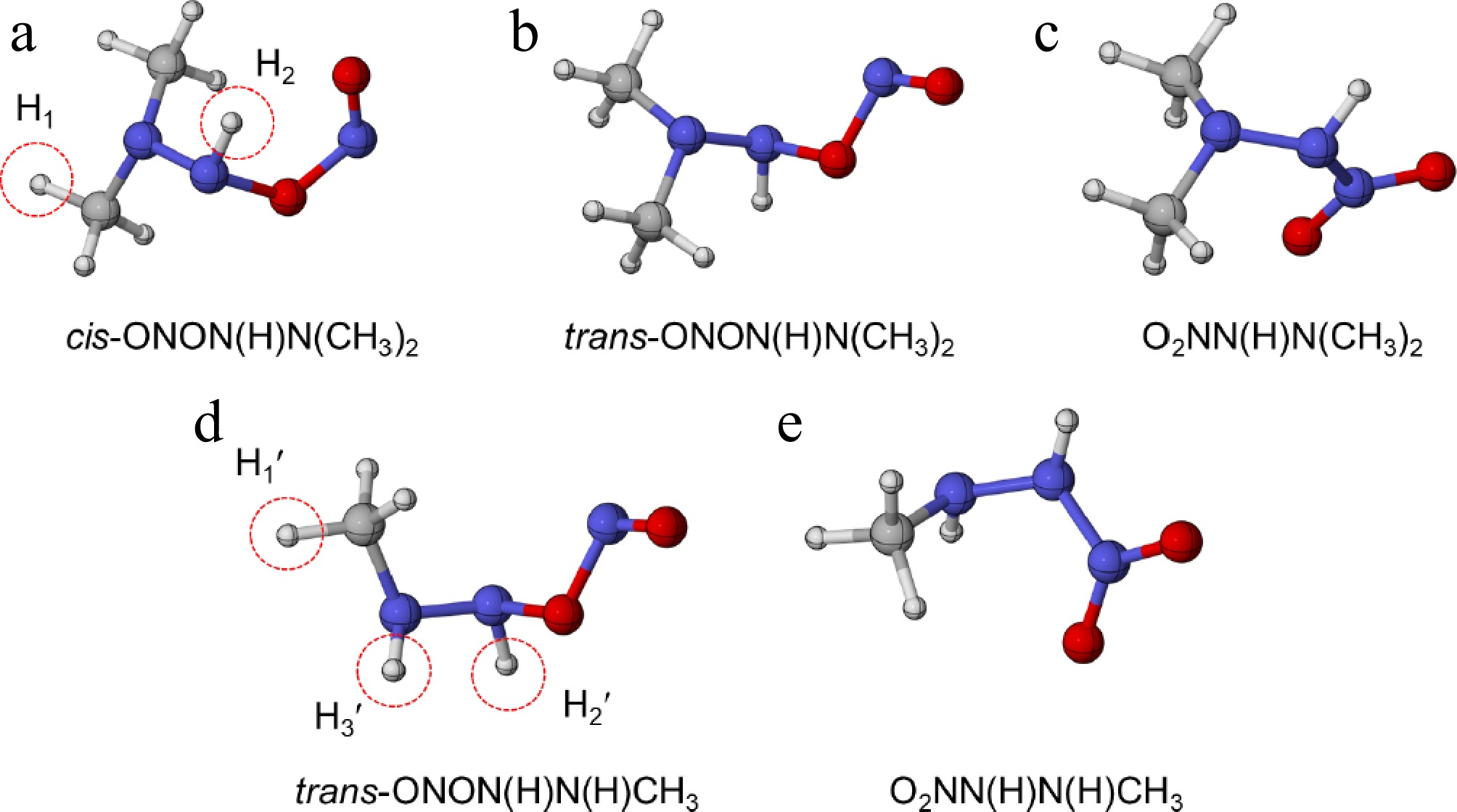
Figure 6. 

The optimized molecular configurations of (a)–(c) HNN(CH₃)₂ + NO₂ at the M06-2X/def2-TZVP level of theory, and (d) NHN(H)CH₃ + NO₂ at the ωB97X-D/6-311++G(d,p) level of theory^[12].

In the HNN(H)CH₃ radical, there are three types of hydrogen atoms: those at the primary carbon sites (H₁′), and those bonded to nitrogen (H₂′ and H₃′). In contrast, the HNN(CH₃)₂ radical lacks H₃′ due to substitution of the H atom by a CH₃ group, retaining only H₁′ and H₂′. Bai et al.^[13] and Kanno et al.^[12] found that reactions of HNN(H)CH₃ with NO₂ primarily produce HNNCH₃ via abstraction of the H atom at H₃′. However, the formation reaction pathways of the related NN(H)CH₃ radical remain unexplored. In HNN(CH₃)₂, this reaction behavior is altered due to the absence of H₃′.

As depicted in Fig. 7, cis-ONON(H)N(CH₃)₂ undergoes a reaction with a low energy barrier of 0.4 kcal/mol, leading to the formation of a product complex (PC) via the abstraction of the H₂′ atom. This product complex ultimately dissociates to generate NN(CH₃)₂ and cis-HONO (R6). In contrast, the decomposition of O₂NN(H)N(CH₃)₂ proceeds via more complex reaction channels. The first pathway requires a relatively high energy barrier of 49.7 kcal/mol to pass through a transition state involving intramolecular H-immigration from the primary carbon site to the O atom of the NO₂ molecule, subsequently generating CH₂NCH₃ and ON(NH)(OH) (R7). In addition, HO₂NNN(CH₃)₂ can be formed from O₂NN(H)N(CH₃)₂ via a relatively low energy barrier of 36.4 kcal/mol. Subsequently, this product decomposes into NN(CH₃)₂ and trans-HONO via a transition state with an energy barrier of 20.5 kcal/mol. Additionally, HO₂NNN(CH₃)₂ undergoes a multi-well reaction pathway, ultimately leading to the formation of CH₂NCH₃ and NN(OH)₂.

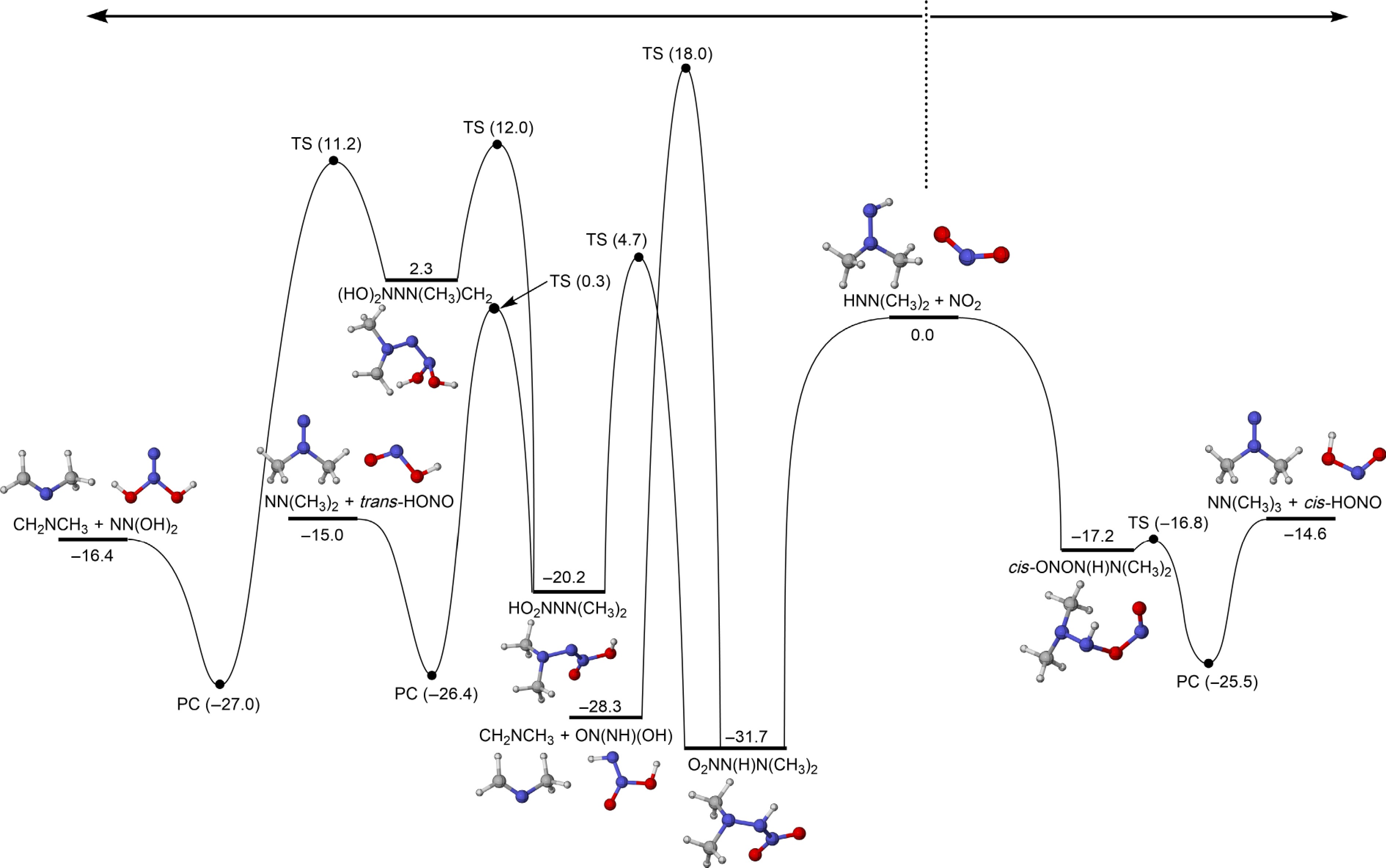
Figure 7. 

PESs for the addition-dissociation reactions of HNN(CH₃)₂ with NO₂ at CCSD(T)/CBS(D+T)//M06-2X/def2-TZVP level of theory (unit: kcal/mol).

Figure 8 shows the rate constants of addition-dissociation reactions of the HNN(CH₃)₂ radical with NO₂ at different pressure conditions. It is evident that the rate constants of reactions R6–R9 decrease with increasing pressure. Particularly, when the temperature is low (300 K), the rate constants of R8 at 0.01 atm and 100 atm differ by as much as six orders of magnitude. In addition, the rate constant of R6 exceeds 1 × 10¹¹ cm³ mol⁻¹ s⁻¹, which is significantly higher than those of the other reactions due to a negative energy barrier. Based on the PES and rate constants, it can be inferred that NN(CH₃)₂ is favorably formed in the addition-dissociation reaction of the HNN(CH₃)₂ radical with NO₂. Vaghjiani et al.^[32] calculated the potential energy surface of the N₂H₃ + NO₂ system, which is more complex compared to the reaction involving HNN(CH₃)₂ and NO₂. For the N₂H₃ + NO₂ system, at low temperatures, the channel leading to the formation of trans-N₂H₂ and trans-HONO is dominant. In contrast, the channel which produces NN(CH₃)₂ + cis-HONO has the most important contribution within the entire temperature range investigated in this work.

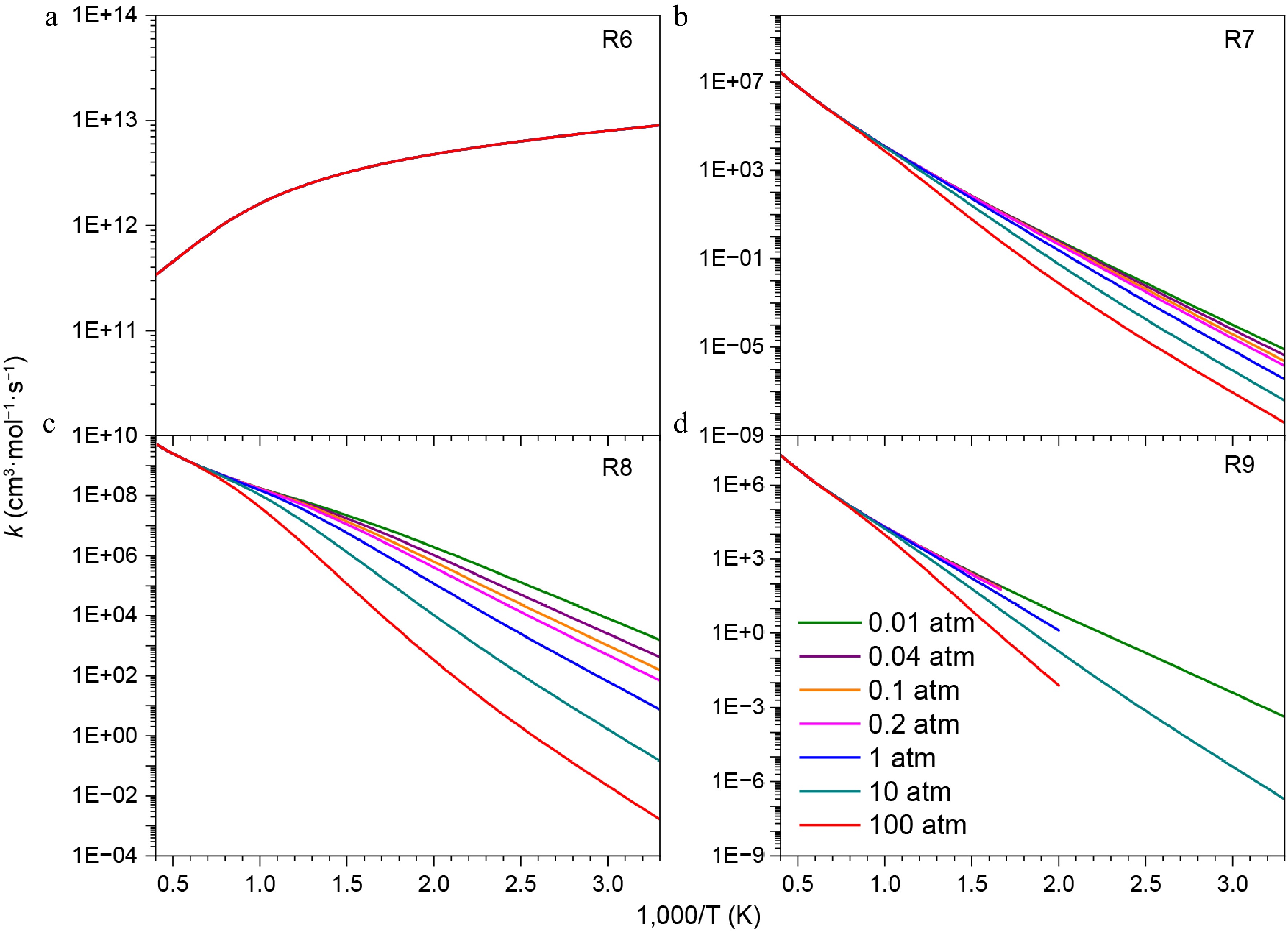
Figure 8. 

Pressure-dependent rate constants for the addition-dissociation reactions of HNN(CH₃)₂ radical with NO₂.

NO attacking

Figure 9 presents the PESs for the addition-dissociation reactions of the HNN(CH₃)₂ radical with the NO molecule. Four reaction pathways are identified based on the resulting products (HNO and NOH). Three intermediates, i.e., ONN(H)N(CH₃)₂-1, ONN(H)N(CH₃)₂-2, and ONN(H)N(CH₃)₂-3, are formed when HNN(CH₃)₂ reacts with NO, releasing 24.7, 22.8, and 23.7 kcal/mol of energy, respectively. For the formation of HNO, there are two main reaction channels. In the first pathway, ONN(H)N(CH₃)₂-1 overcomes an energy barrier of 41.1 kcal/mol, then the formed product complex decomposes into NN(CH₃)₂ and HNO (R10). The second pathway requires a relatively higher energy barrier of 45.8 kcal/mol and leads to the transformation of ONN(H)N(CH₃)₂-1 into HNN(CH₃)CH₂ and HNO (R11). For NOH formation, ONN(H)N(CH₃)₂-3 proceeds through a three-membered transition state with an energy barrier of 66.7 kcal/mol to form NN(CH₃)₂ and NOH (R12). The entire process requires a total energy input of 82.0 kcal/mol, which is higher than that of the other three reactions. When the O atom of NO attacks the H atom at the primary carbon (R14) directly, the energy barrier of the H-abstraction reaction is 48.6 kcal/mol, and the overall energy required to form HNN(CH₃)CH₂ and NOH (R13) is 56.8 kcal/mol.

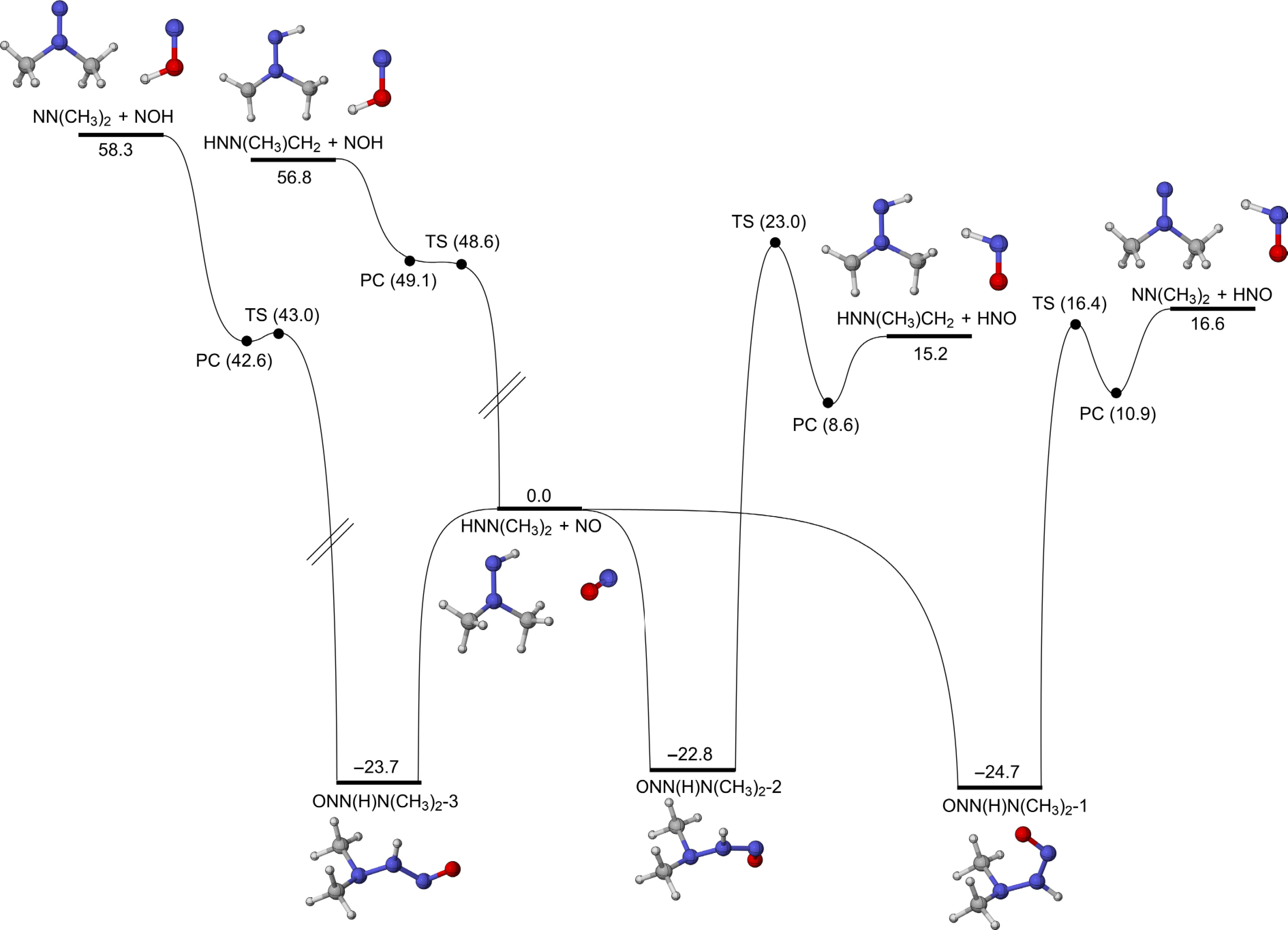
Figure 9. 

PESs for the addition-dissociation reactions of HNN(CH₃)₂ with NO at CCSD(T)/CBS(D+T)//M06-2X/def2-TZVP level of theory (unit: kcal/mol).

Figure 10 shows the rate constants for the addition-dissociation reactions of HNN(CH₃)₂ with the NO molecule based on the PES results. It is evident that reactions R12 and R13 exhibit lower rate constants due to their higher energy barriers. R10 has the lowest barrier among the four reactions, demonstrating the highest reaction rate. As the reaction temperature increases, the differences in rate constants among the four reactions gradually decrease. As depicted in Fig. 10b, the branching ratio of R10 decreases with increasing temperature and reaches 70% at 2,500 K. Another HNO formation reaction (R11) plays a secondary role in the addition-dissociation reactions of HNN(CH₃)₂ with NO. In addition, the NOH formation reactions make smaller contributions. According to the calculated results for the addition-dissociation reactions of HNN(CH₃)₂ with NO₂ and NO, it can be concluded that NN(CH₃)₂ is readily formed.

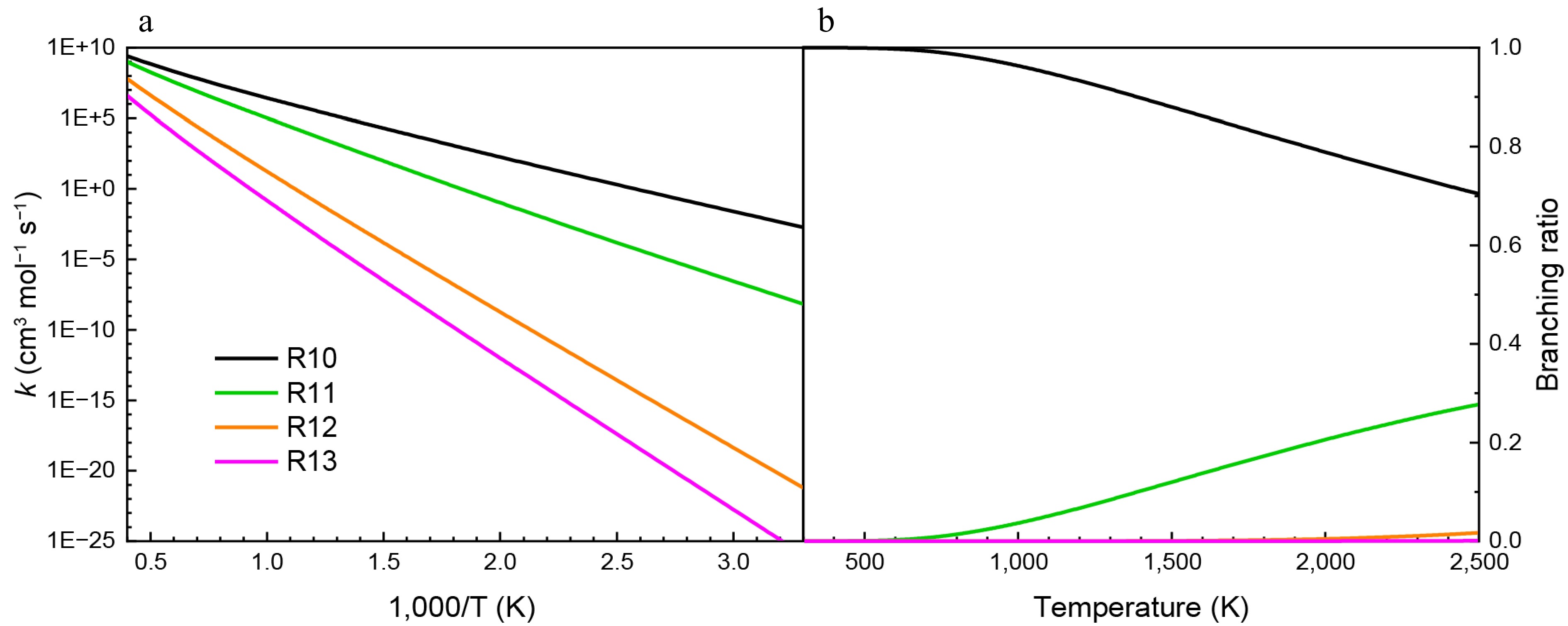
Figure 10. 

(a) Rate constants, and (b) branching ratios for the addition-dissociation reactions of HNN(CH₃)₂ with NO at HPL.

Subsequent decomposition reactions of NN(CH₃)₂

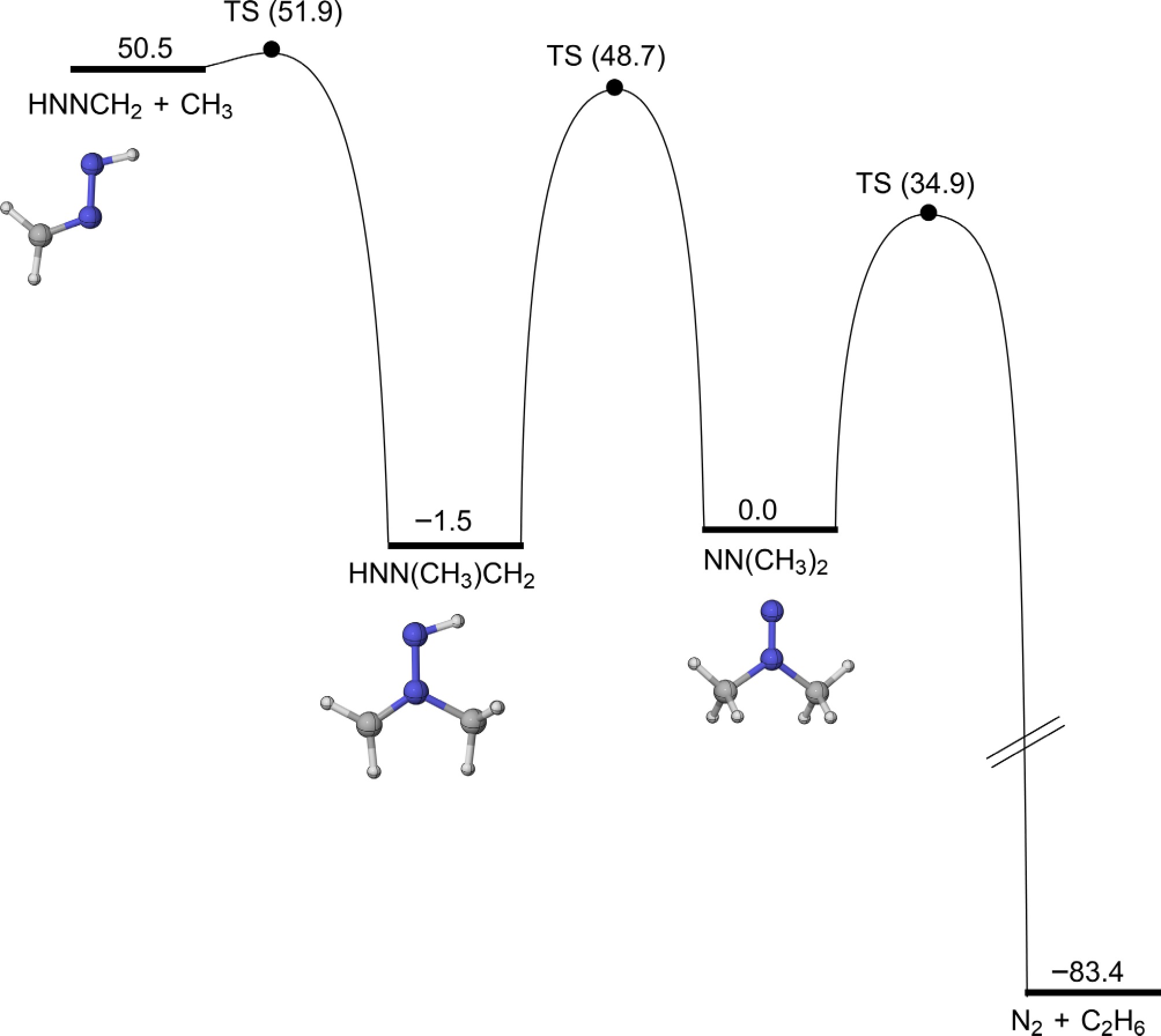
Considering that NN(CH₃)₂ is easy to form, its subsequent consumption reactions were studied. As shown in Fig. 11, the H-migration isomerization reaction (R14) of NN(CH₃)₂ to generate the HNN(CH₃)CH₂ radical has an energy barrier of 48.7 kcal/mol. The calculations also indicate that NN(CH₃)₂ can dissociate to produce N₂ and C₂H₆ (R15), with an energy barrier of 34.9 kcal/mol and releasing 83.4 kcal/mol of energy. This barrier is 13.8 kcal/mol lower than that of the H-migration isomerization reaction, making R15 the more favorable pathway. In addition, the β-N-C scission of the HNN(CH₃)CH₂ radical to form HNNCH₂ and CH₃ (R16) has a higher energy barrier of 53.4 kcal/mol. Rate constant calculations under varying pressures, as presented in Fig. 12, further demonstrate that R15 has a higher rate constant, as a result of its relatively lower energy barrier. Furthermore, the rate constants of R14 and its reverse reaction (R14-R) exhibit strong pressure dependence, particularly at high temperatures, whereas the pressure effects on R15 and R16 are comparatively weaker, especially at lower temperatures.

Figure 11. 

PESs for the isomerizartion and β-scission reactions of NN(CH₃)₂ at CCSD(T)/CBS(D+T)//M06-2X/def2-TZVP level of theory (unit: kcal/mol).

Figure 12. 

Pressure-dependent rate constants for the consumption reactions of NN(CH₃)₂.

In this work, the decomposition reactions of HNN(CH₃)₂ radical, including the isomerization, β-scission, and H-abstraction reactions, were theoretically investigated at the CCSD(T)/CBS(D+T)//M06-2X/def2-TZVP level of theory. Pressure-dependent rate constants of isomerization and β-scission reactions of HNN(CH₃)₂ were determined by solving the RRKM/ME equations. Additionally, the subsequent decomposition reactions of NN(CH₃)₂ were also studied. Comparative analyses with MMH radicals were conducted to elucidate the effects of CH₃ group substitution on the kinetic characteristics of UDMH radical decomposition. The key findings can be summarized as follows:

(1) For the isomerization and β-scission reactions of UDMH radicals, HNN(CH₃)₂ undergoes β-scission (forming HNNCH₃) more readily than H-migration isomerization. For the H₂NN(CH₃)CH₂ radical, the β-N-N scission reaction that produces CH₂NCH₃ and NH₂ is characterized by a relatively lower energy barrier and a higher rate constant.

(2) For the H-abstraction reactions of HNN(CH₃)₂ by NO₂, the pathway forming NN(CH₃)₂ and cis-HONO via the decomposition of cis-ONON(H)N(CH₃)₂ has the lowest energy barrier and the highest rate constants. Similarly, H-abstraction by NO also readily yields NN(CH₃)₂. Subsequently, NN(CH₃)₂ dissociates into N₂ and C₂H₆ through a pathway with a relatively low energy barrier.

(3) Based on the comparison, the kinetic properties of β-scission reactions in UDMH radicals are similar to those in MMH radicals. However, the H-abstraction of HNN(CH₃)₂ by NO₂ differs significantly from that of the MMH radical (HNN(H)CH₃). HNN(CH₃)₂ primarily undergoes H-abstraction at the terminal nitrogen site to form NN(CH₃)₂, whereas HNN(H)CH₃ favors H-abstraction from the central nitrogen atom. The obtained fundamental kinetic parameters provide critical inputs for refining detailed chemical kinetic models of hydrazine-based propellant combustion.