Data-driven design of electromagnetic functional materials: a statistical perspective

The rapid development of radar stealth, 5G communications, electromagnetic interference shielding, and flexible electronics has significantly elevated the importance of electromagnetic functional materials in critical domains including information technology, energy, defense, and intelligent manufacturing^[1,2]. These advanced materials must simultaneously demonstrate optimal dielectric properties, magnetic permeability, impedance matching characteristics, and broadband absorption performance while maintaining stable responses under complex multi-physics conditions involving temperature fluctuations, frequency variations, and electric field interactions^[3,4]. Nevertheless, substantial challenges persist due to intricate material architectures, multifactorial performance dependencies, protracted experimental cycles, and extensive parameter spaces^[5]. These complexities have rendered conventional empirical approaches and single-variable analysis methodologies increasingly inadequate for addressing contemporary engineering requirements. Consequently, the development of systematic, precise, and efficient theoretical frameworks for predictive design, mechanistic understanding, and performance optimization has emerged as a paramount research objective in this field.

In recent years, statistical methodologies—have also been referred to as data-driven design approaches^[6]. In the context of this review, statistical methodologies are defined as an overarching framework encompassing classical statistical tools (e.g., regression analysis, variance testing), statistical modeling paradigms (e.g., Bayesian inference, nonparametric kernel methods), and modern machine learning and deep learning algorithms. Machine learning is here regarded as a subset of statistical methodologies, with algorithms such as random forests^[7,8], support vector machines, Gaussian process regression^[9], and gradient boosting trees^[10] widely applied to materials research. More recently, deep learning architectures including convolutional neural networks (CNN), residual networks (ResNet), and generative adversarial networks (GAN) have been introduced for tasks such as property prediction, structure optimization, and rapid inverse design of metamaterials, thereby extending the predictive and design capabilities of data-driven frameworks. These statistical models now enable comprehensive research capabilities spanning material performance prediction, structural optimization, mechanism identification, parameter inversion, and efficient simulation. For electromagnetic functional materials specifically, statistical methodologies have not only substantially enhanced the efficiency of material design and performance modulation but have also created new pathways for deciphering complex physical mechanisms and establishing structure–performance–function relationships^[11,12].

This review is structured around statistical methodologies to systematically survey their applications in the design and performance optimization of electromagnetic functional materials. We begin with an in-depth examination of innovative implementations of statistical methodologies across three core research themes: electromagnetic performance prediction, Electromagnetic Mechanism Modeling, and Parameter Inversion & Rapid Simulation. Subsequently, representative case studies within each thematic direction are systematically compiled, demonstrating the pivotal role of statistics-driven approaches in addressing complex electromagnetic challenges. The review also identifies persisting challenges associated with statistical methodologies, including limitations in model generalizability, cross-system adaptability, and handling of high-dimensional multivariate problems. Through this synthesized overview, we aim it to serve as a systematic reference and provide guidance for performance enhancement, mechanistic interpretation, and inverse design in electromagnetic functional materials.

As applications of electromagnetic functional materials expand into advanced communication, intelligent manufacturing, and energy technologies, the design and optimization of their performance are increasingly hindered by high-dimensional parameter spaces, multiphysics coupling, and complex nonlinear responses. Traditional physical modeling and empirical approaches have increasingly exhibited limitations in accuracy and generalizability, especially when applied to emerging material systems characterized by intricate structures and diverse property demands. Statistics, as a mathematical paradigm that integrates probabilistic inference and data-driven modeling, provide a rigorous theoretical foundation and powerful tools for uncertainty quantification, offering distinct advantages in addressing the complexity bottlenecks in modern materials science.

This section provides a systematic overview of prevailing statistical frameworks, organized according to three principal modeling contexts that are further elaborated in subsequent chapters: performance prediction, mechanism discovery, and inverse design. By aligning key equations with representative material examples, the discussion highlights the methodological connections between theoretical formulations and their applications in materials research.

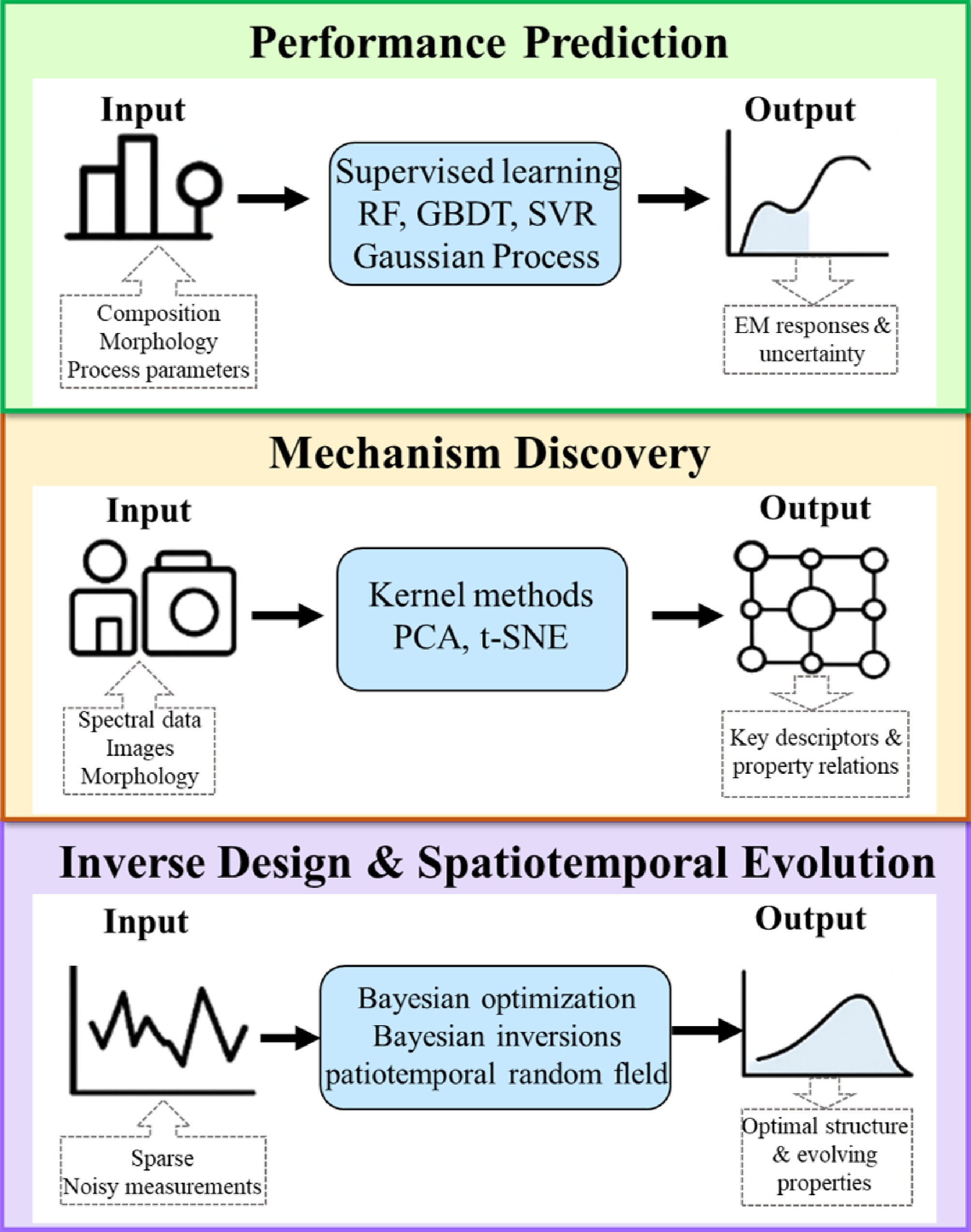
In recent years, the application of statistical methodologies in the study of electromagnetic materials has evolved along three principal directions (Fig. 1) ; (i) Performance prediction. This research avenue primarily employs regularized supervised learning and Gaussian process regression (Eqs [1]–[6]) to establish predictive mappings between complex input variables—including composition, morphology, and processing parameters—and electromagnetic responses. In addition to predictive accuracy, these approaches incorporate uncertainty quantification, thereby improving the efficiency and reliability of both experimental characterization and numerical simulation^[13,14]; (ii) Mechanism discovery. Methods such as kernel techniques, principal component analysis (PCA), and t-distributed stochastic neighbor embedding (t-SNE; Eqs [7]–[12]) are widely used to extract interpretable low-dimensional features from spectral, imaging, or morphological datasets. These representations enable the identification of structure–property relationships and provide mechanistic insights into material behavior^[15−18]; (iii) Parameter inversion and rapid simulation. This direction integrates design-of-experiments strategies, Bayesian inversion, and random-field or spatiotemporal covariance models (Eqs [13]–[15]), with the goal of identifying optimal microstructural parameters under sparse or noisy data conditions and predicting long-term material performance in heterogeneous spatiotemporal environments^[19−22].

Figure 1. 

Conceptual framework of statistical approaches in electromagnetic functional materials.

Beyond these three pillars, emerging paradigms such as generative modeling, representation learning, and graph neural networks are increasingly broadening the scope of statistical approaches in this field. Nevertheless, the triad of performance prediction, mechanism discovery, and inverse design continues to provide the dominant framework for contemporary research on statistical methods in electromagnetic materials.

Electromagnetic performance prediction

Performance prediction from composition, microstructure, and processing descriptors represents a central theme in materials informatics. Formally, the task can be framed as learning a mapping:

where, the input x encodes high-dimensional descriptors (composition vectors, morphological descriptors, processing parameters, etc.) and the output y denotes one or more figures of merit such as absorption bandwidth, reflection loss, shielding effectiveness, or frequency-dependent S-parameters. Practical difficulties include high dimensionality and collinearity among inputs, heteroscedastic or limited data, and the necessity of calibrated uncertainty quantification to support experimental decision-making.

To address these challenges, three classes of statistical strategies are particularly influential: (i) regularized empirical-risk formulations to control model complexity; (ii) flexible nonparametric or supervised learners capable of capturing nonlinear structure; and (iii) probabilistic surrogate models that provide principled uncertainty estimates. A unifying principle is regularized empirical risk minimization^[23,24],

where, L denotes a task-appropriate loss (e.g., squared error for regression), $ \mathrm{\Omega }\left(\theta \right) $ a complexity penalty (e.g., ℓ2 or ℓ1 norms), and $ \lambda \ge 0 $ a regularization parameter. Equation (2.1) subsumes classical linear regularization (ridge, lasso), kernel methods, and—conceptually—many ensemble and iterative algorithms whose implicit regularization (pruning, shrinkage, early stopping) controls complexity.

For a linear predictor $ {f}_{\theta }\left(x\right)={x}^{\mathrm{\top }}\theta $ with ℓ2 penalty, the ridge solution admits a closed form:

with $ X\in {\mathbb{R}}^{n\times p} $ the design matrix and $ y\in {\mathbb{R}}^{n} $ the response vector. The lasso(ℓ1) variant promotes sparsity in $ \theta $ and is solved via convex optimization; its statistical behaviors is well studied in high-dimensional regimes. Kernel ridge regression (the dual form of ridge) and support-vector regression extend these linear ideas to nonlinear feature maps via kernels^[25−27].

In practical, tabular-materials settings, tree-based ensemble methods (random forests, gradient-boosted trees, XGBoost, LightGBM) are widely adopted because they naturally handle mixed-type descriptors and are robust to feature collinearity^[28]. Their hyperparameters and generalization performance are typically assessed by K-fold cross-validation; model selection and hyperparameter tuning should report both point-prediction metrics (RMSE, R²) and uncertainty-sensitive diagnostics (e.g., predictive interval coverage) when stakes justify.

When calibrated uncertainty quantification is required—for active learning, Bayesian optimization, or risk-aware decision making—Gaussian process regression (GPR) is a principled probabilistic surrogate^[29,30]. A standard GPR model places a Gaussian process prior on f and assumes Gaussian observation noise:

with kernel k parametrized by $ {\theta }_{k} $ and noise variance $ {\sigma }_{n}^{2} $. Given data $ \mathcal{D}=\left\{\right({x}_{i},{y}_{i}){\}}_{i=1}^{n} $, the posterior predictive distribution at x_* is Gaussian with mean and covariance:

where, $ K=\left[k\right({x}_{i},{x}_{j}){]}_{i,j=1}^{n} $, $ {k}_{*}=[k({x}_{*},{x}_{i}){]}_{i=1}^{n} $, $ {k}_{**}=k({x}_{*},{x}_{*}) $. The predictive variance given by $ {\mathrm{\Sigma }}_{*}\left({x}_{*}\right) $ furnishes principled credible intervals that are critical for experimental planning and exploration–exploitation trade-offs.

Hyperparameters $ ({\theta }_{k},{\sigma }_{n}^{2}) $ are commonly estimated by marginal likelihood maximization:

which balances model fit against complexity in a data-driven manner. For large n, scalable GP approximations (inducing points, sparse variational GPs, kernel interpolation) are used to reduce computational cost from $ \mathcal{O}({n}^{3}) $ to near-linear regimes^[31−34].

Deep learning models—when sufficiently large labelled datasets or raw spectral/image inputs are available—offer powerful representation learning capabilities (convolutional architectures for imagery/spectra, fully connected nets for engineered descriptors). However, they require careful regularization, calibration of predictive uncertainty (e.g., via Bayesian neural networks, deep ensembles, or post-hoc calibration), and interpretability procedures before being integrated into experimental design loops^[35−37].

A practical workflow often combines complementary methods: ensembles or gradient-boosted trees serve as accurate baseline predictors on tabular descriptors; GPRs or other Bayesian surrogates are used for uncertainty-aware optimization and active learning^[38,39]; and representation learning (deep models) is employed where raw high-dimensional inputs (images, spectra) are available. Model evaluation should therefore report both accuracy metrics and uncertainty calibration diagnostics (predictive interval coverage, width), and cross-validation procedures must be carefully designed to avoid selection bias, especially when sample sizes are limited^[40,41].

Electromagnetic mechanism modeling

Understanding how micro- and nano-scale structures influence macroscopic electromagnetic properties are a central challenge in materials science. Mechanism discovery seeks to extract interpretable patterns and quantitative relationships from high-dimensional structural, spectral, or morphological data, providing insights that go beyond mere performance prediction.

Kernel-based methods provide a flexible, nonparametric framework for modeling complex, nonlinear structure–property relationships. By mapping the input x into a high-dimensional feature space through a positive-definite kernel function $ k(x,{x'}) $, linear regression or classification becomes feasible in this implicit space. The resulting model can be expressed as:

where, $ \lambda $ controls regularization. Common kernels include the radial basis function:

and the polynomial kernel:

In addition to enabling nonlinear regression or classification, the kernel-induced feature space can be analyzed to identify key structural descriptors that drive electromagnetic behavior. These kernel-based models, applied in support vector machine regression or classification tasks, provide a statistically robust framework for detecting structure–property boundaries, such as correlations between pore circularity and microwave absorption^[42−44].

Dimensionality reduction techniques complement kernel methods by compressing high-dimensional spectral, image, or morphological data into low-dimensional, interpretable representations while preserving essential variance. Principal component analysis (PCA) identifies orthogonal directions W that maximize the ratio of between-class to within-class variance:

with the corresponding generalized eigenvalue problem yielding the dominant components.

In practice, PCA can reduce high-dimensional spectral measurements, such as MXene dielectric spectra, to a few principal components, highlighting features (e.g., dielectric loss factors $ {\text ϵ}'' $at 8–12 GHz most relevant to absorption performance)^[45,46]. For visualization and exploratory analysis, t-distributed stochastic neighbor embedding (t-SNE) maps high-dimensional pairwise similarities to a low-dimensional manifold by minimizing the Kullback–Leibler divergence:

revealing clusters corresponding to distinct microstructural morphologies. While PCA provides linearly interpretable principal components, t-SNE complements this by capturing local nonlinear structures, making the low-dimensional representation suitable for visualization and mechanistic interpretation^[46,47].

Equations (7)–(12) collectively establish the mathematical foundation for Electromagnetic Mechanism Modeling. Kernel-based methods capture nonlinear dependencies between structural descriptors and electromagnetic performance, while PCA and t-SNE generate compact, interpretable features^[45,46,48]. Together, these approaches transform raw high-dimensional spectra or images into quantitative insights, enabling the identification of specific microstructural traits that govern macroscopic electromagnetic behavior and facilitating subsequent linkage of structure to function in a statistically robust manner.

Parameter inversion and rapid simulation

Electromagnetic devices frequently operate under spatially heterogeneous and temporally evolving conditions, while experimental observations are often sparse due to cost or accessibility constraints. In this context, inverse design and spatiotemporal modeling provide systematic frameworks to: (i) identify optimal microstructural or material parameters with minimal experimental effort; and (ii) predict long-term electromagnetic performance across spatial domains^[49−51].

Bayesian optimization treats the design objective $ y\left(x\right) $ as a realization of a Gaussian process, where the acquisition function:

balances exploitation (high posterior mean) and exploration (high posterior uncertainty). Sequential maximization of $ \alpha \left(x\right) $ guides subsequent experiments or simulations toward the most informative regions of the design space. This framework has been demonstrated to efficiently determine optimal parameters of gradient-impedance absorbers, achieving targeted reflection loss with a fracti on of the full factorial experimental grid^[49,52].

For parameter retrieval under measurement noise, Bayesian inversion quantifies uncertainty in material parameters m given observed responses.

where, the likelihood $ p({d}_{obs}\mid m) $ accounts for forward-model uncertainty and measurement noise, and the prior $ \pi \left(m\right) $ encodes structural or material constraints. Markov-chain Monte Carlo sampling of Eq. (14) provides credible intervals for material properties such as permittivity and permeability, enabling uncertainty-aware design and validation^[53].

Spatiotemporal evolution of electromagnetic properties can be captured using random-field modeling, where thermal or oxidative aging is represented via a separable covariance function:

with spatial lag $h $, temporal lag $ \tau $, and correlation lengths $ {\lambda }_{s} $, $ {\lambda }_{t} $ estimated by restricted maximum likelihood. Kriging with Eq. (15) interpolates sparse measurements, generating spatial maps of property evolution, while incorporation into state-space or ARIMA models enables short-term forecasting, guiding maintenance schedules or component replacement^[54].

Equations (13)–(15) collectively define the methodological framework for Parameter Inversion and Rapid Simulation. Bayesian optimization efficiently explores the design space, Bayesian inversion quantifies parameter uncertainty, and random-field modeling captures spatiotemporal variability. Together, these approaches facilitate a statistically principled transition from limited measurements to spatially and temporally resolved predictions, supporting design, validation, and long-term performance assessment in electromagnetic materials.

In summary, a coherent framework emerges for the data-driven analysis and design of electromagnetic materials. Statistical and machine-learning models enable robust prediction of macroscopic properties from compositional, microstructural, and processing descriptors. Complementary mechanism discovery approaches extract low-dimensional, interpretable representations that clarify structure–property relationships, while inverse design and spatiotemporal modeling provides strategies to explore optimal designs, quantify uncertainty, and anticipate material behavior over space and time. Together, these methodologies offer a unified perspective on how statistical theories can guide understanding, prediction, and rational design in the field of electromagnetic functional materials. The next section discusses concrete applications of these statistical frameworks, illustrating their effectiveness across different material systems and performance metrics.

Accurately and efficiently predicting key performance metrics—such as microwave absorption efficiency, electrical conductivity, and bandwidth response—remains a central challenge in the design of electromagnetic functional materials. In recent years, data-driven statistical methodologies, particularly those grounded in machine learning, have demonstrated significant promise in performance forecasting and structural optimization. Compared with conventional empirical trial-and-error approaches, these methods not only enhance research efficiency but also catalyze a paradigm shift toward intelligent and systematic materials design. Depending on the size of datasets, feature types, and the complexity of physical descriptors, a diverse range of models—from ensemble learning and probabilistic regression to evolutionary algorithms and deep neural networks—have been developed to address these challenges.

Electromagnetic performance prediction

Random forest (RF) and other ensemble learning models have been widely adopted to capture nonlinear interactions among structural and compositional descriptors. For example, Ding et al. optimized the terahertz absorption bandwidth of patterned graphene metasurfaces (PGMAs) using an RF-based framework trained on 500 FDTD simulations, achieving superior accuracy over linear regression (LR) and support vector machines (SVM) (R² = 0.938 at the 90% absorption threshold) with optimization time reduced from days to under 30 min (Fig. 2a–c)^[11]. Similarly, Zhang et al. introduced DCPRO, a random forest regression model for flexible BaTiO₃/rGO/PDMS composites, where SHAP analysis revealed frequency and hydrazine dosage as dominant factors in governing dielectric performance. The model achieved an R² above 0.99 for the real part of permittivity and guided the design of broadband absorbers with reflection losses down to –56.08 dB (Fig. 2d, e)^[55]. In the domain of conductivity, Gao et al. established the OMC-CD dataset covering 219 2D organic metal chalcogenides, and SVM models provided the most accurate classification of conductivity regimes, achieving up to 96.6% accuracy. Ligand identity was identified as the most critical determinant of conductivity (Fig. 2f)^[12].

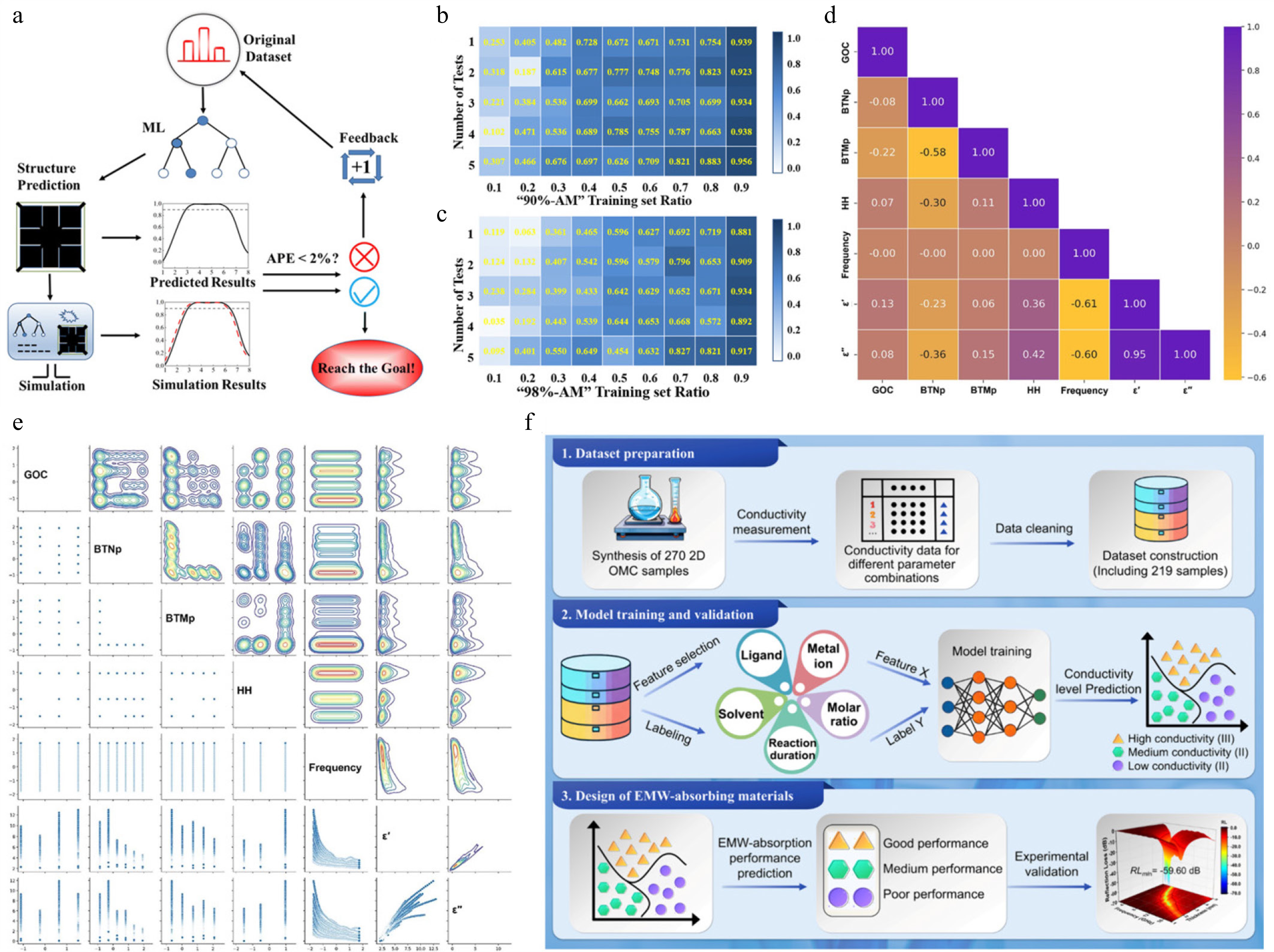
Figure 2. 

(a) Schematic illustration of the machine learning–assisted prediction workflow for optimizing metasurface structural parameters. (b), (c) Coefficients of determination (R²) under varying training set proportions^[11]. (d) Heat map of Pearson correlation coefficients between input features and output variables. (e) Correlation matrix of input features with dielectric properties, visualized through scatterplots. Diagonals show feature distributions^[55]. (f) Machine learning strategy for conductivity prediction and electromagnetic wave absorber design in 2D ordered mesoporous carbons (OMCs)^[12].

Evolutionary algorithms and probabilistic regression have further extended the capability of statistical methodologies to materials with complex structures or limited datasets. Wang et al. applied a genetic algorithm (GA) combined with a transmission line model to design hierarchical SiC@SiO₂ nanowire aerogels, identifying gradient-impedance architectures that achieved full-band absorption across 2–18 GHz^[56]. Similarly, Bora et al. leveraged Gaussian Process Regression (GPR) to model PDMS/Fe₂O₃ nanocomposites using only four data points, with uncertainty quantification enabling accurate extrapolation and guiding experimental synthesis of composites achieving –63 dB reflection loss (Fig. 3a–c)^[57]. These approaches highlight the adaptability of statistical methodologies to varying data availability and design complexity.

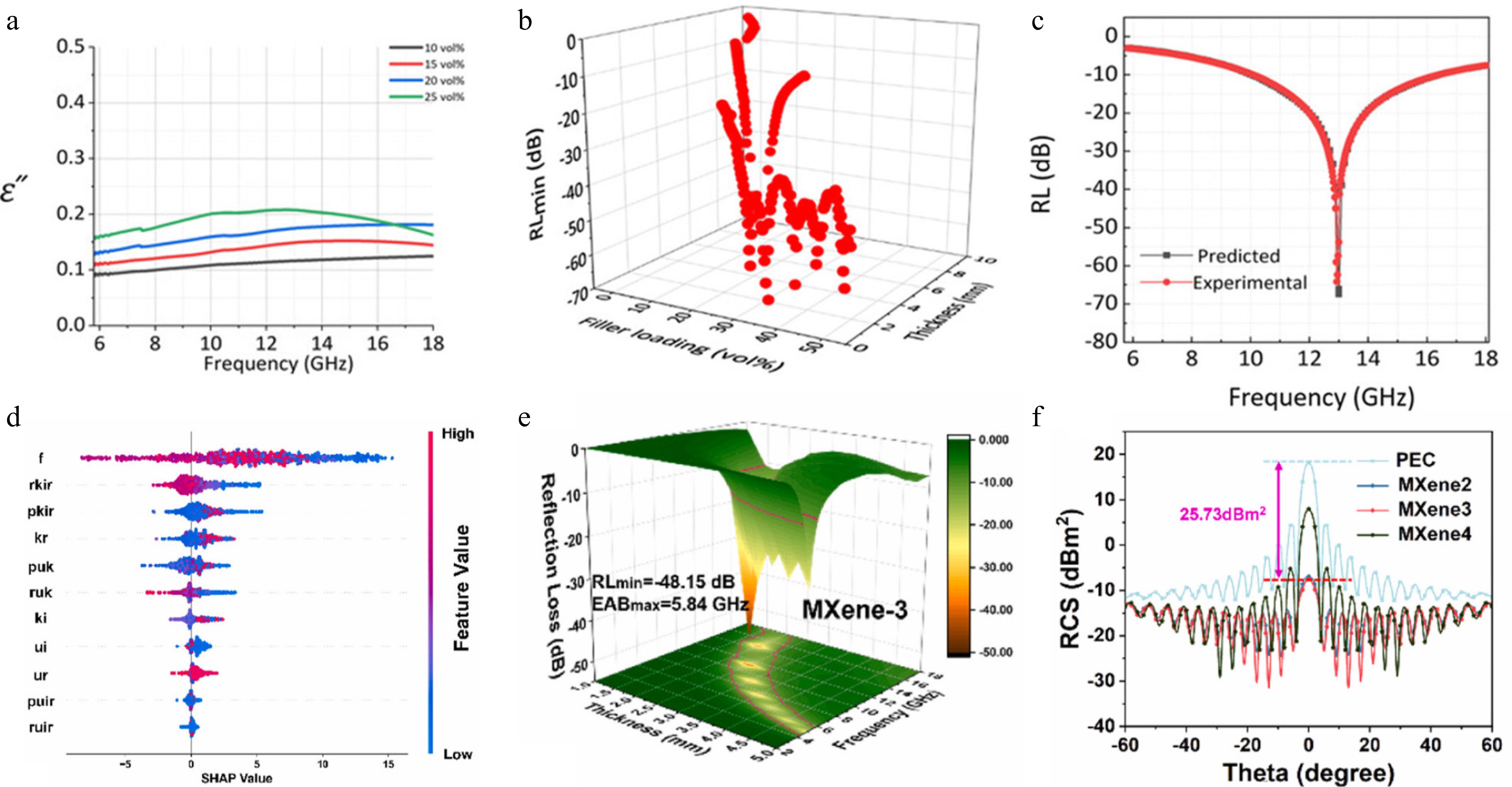
Figure 3. 

(a) Measured dielectric permittivity of Fe₂O₃-loaded PDMS nanocomposites^[57]. (b) Predicted minimum reflection loss (RL_min) of PDMS nanocomposites with varying Fe₂O₃ nanoparticle loadings (0.1–50 vol%) at their optimal thicknesses. (c) Comparison between predicted and experimentally measured reflection loss values^[58]. (d) Relationship between feature variables and their SHAP values as computed by the regression model. (e) Three-dimensional plots of reflection loss for the MXene-3 sample. (f) Simulated radar cross-section (RCS) curves of bare PEC vs PEC coated with the absorbing layer^[59].

In high-dimensional compositional spaces, ensemble learning methods such as gradient boosting regression (GBR) have proven effective in identifying key variables and guiding material synthesis. Liu et al. analyzed 74 high-entropy spinel ferrite absorbers using 34 descriptors, where GBR combined with SHAP analysis revealed critical doping factors and directed the synthesis of optimized compositions^[58]. Zhou et al. applied a LightGBM classifier to MXene absorbers, achieving near-perfect classification (AUC = 0.99) and guiding multilayer design that reduced radar cross section by over 25 dB·m² (Fig. 3d–f)^[59].

More recently, deep neural networks have expanded the capability of data-driven design to directly handle image-like structural representations, bypassing explicit feature engineering. For instance, in the predictive modeling of MXene-based solar absorbers, a deformable convolutional neural network (CNN) was trained on geometric images to achieve high-accuracy spectrum prediction. By integrating Grad-CAM visualization, the model identified critical regions within absorber geometries, enabling targeted optimization. Importantly, this approach replaced time-consuming FDTD/FEM simulations with rapid geometry-to-spectrum mapping, significantly shortening the design cycle for MXene–MIM absorbers^[60].

Collectively, these studies demonstrate that statistical methodologies—from ensemble learning to deep neural networks—provide a powerful toolbox for performance prediction and structural optimization of electromagnetic functional materials. Traditional machine learning excels in small to medium-scale datasets with interpretable descriptors, probabilistic and evolutionary methods address uncertainty and structural search, while deep learning uniquely enables direct handling of complex geometries and rapid spectrum prediction. Together, these approaches are driving a methodological shift from empirically guided discovery toward predictive, data-driven, and high-throughput materials design.

Electromagnetic mechanism modeling

Beyond performance prediction, statistical modeling has become pivotal in uncovering microscopic loss mechanisms, interfacial charge dynamics, and structure–property relationships in electromagnetic functional materials. These approaches are driving a shift from passive property optimization toward mechanistic control and programmable regulation. By integrating interpretable models, researchers can now construct synergistic frameworks that link material structure, underlying mechanisms, and resulting performance, enabling more rational design strategies.

In metal single-atom systems, Yuan et al.^[5] applied machine learning to establish structure–property mappings through a multidimensional database encoding atomic species, coordination configurations, and geometric descriptors. A Random Forest model quantitatively captured how different single-atom configurations affect dielectric loss behavior (Fig. 4a–c), revealing pronounced nonlinear coupling between coordination environments and polarization relaxation. Model-guided screening identified optimal configurations, which were experimentally validated to enhance absorption. First-principles calculations confirmed that single-atom doping reconstructs the local electronic structure and enhances interfacial dipolar polarization (Fig. 4d). This study exemplifies how statistical modeling can close the loop from modeling → inference → validation, providing quantitative guidance for mechanism-driven interface engineering.

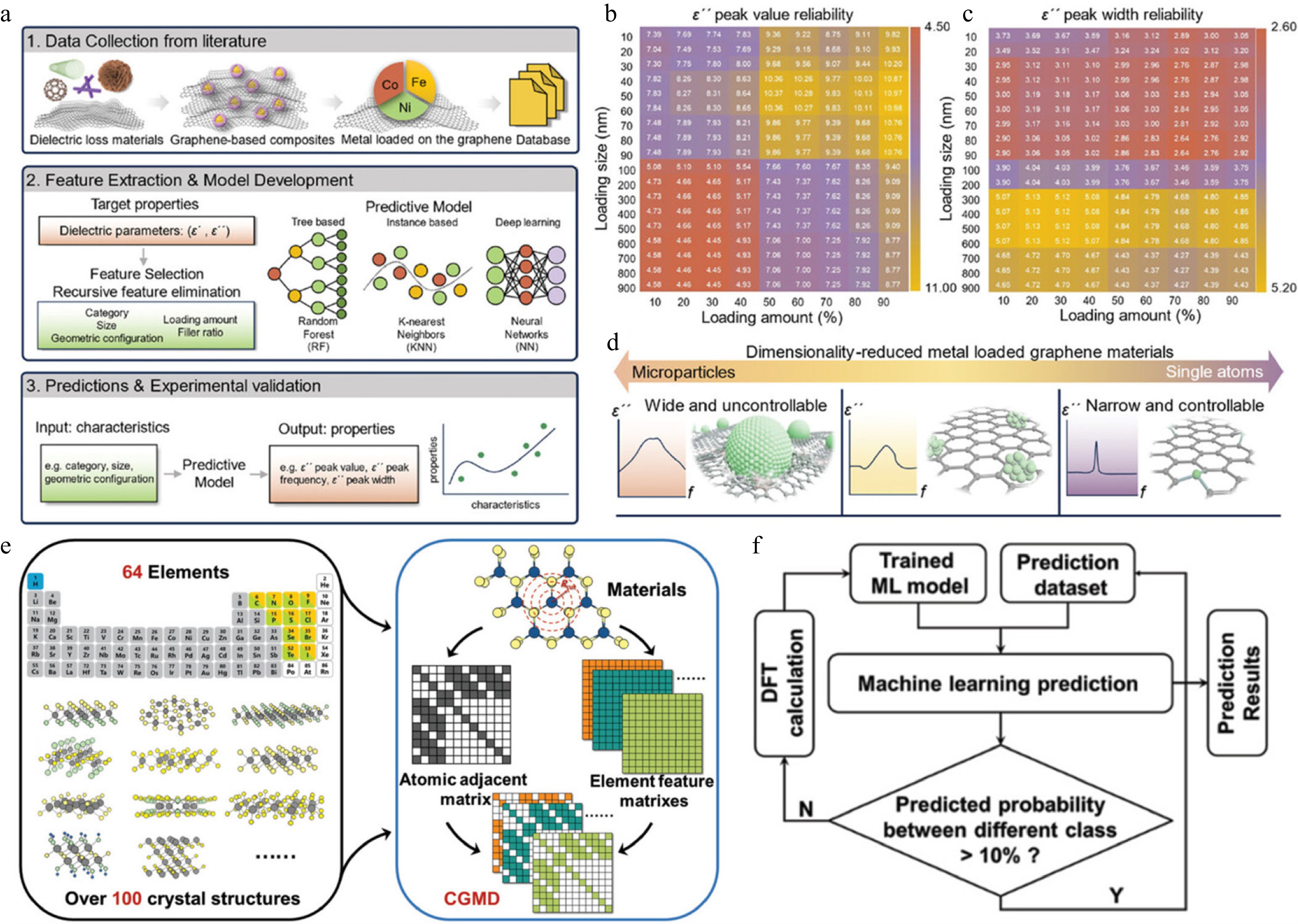
Figure 4. 

(a) Workflow for predicting the relationship between material descriptors and dielectric loss parameters. (b) Reliability of ε peak values for Co/graphene composites at 50% loading. (c) Reliability of peak widths under the same condition. (d) Influence of metal loading size on dielectric loss parameters in graphene-based materials^[5]. (e) Schematic of the Crystal Graph Multilayer Descriptor (CGMD) computation. (f) Iterative machine learning feedback loop for active materials discovery^[61].

For high-throughput screening of two-dimensional magnetic materials, Lu et al. developed a crystal graph multilayer descriptor (CGMD) integrated with an active learning strategy to iteratively discover 2D ferromagnetic semiconductors, half-metals, and metals (Fig. 4e, f)^[61]. CGMD encodes crystal topology and elemental physicochemical properties into high-dimensional tensors, enabling generalization across structurally diverse datasets. With 1,459 training materials and 3,759 candidates for prediction, the framework identified 93 promising 2D materials, and layer-wise analysis linked microscopic descriptors such as Mendeleev number and unpaired electron count to magnetic behavior. This interpretable approach has also been extended to MXenes for multi-objective screening of both thermodynamic stability and electronic properties^[62].

Traditional statistical inference remains essential for analyzing microscopic electromagnetic loss. Cao et al. examined graphene–silica aerogel composites by decomposing ε″ into polarization (ε_p″) and conductive loss (ε_c″) components. Variable-temperature experiments revealed a competition between dipole rotation and charge carrier excitation (Fig. 5a, b)^[63]. By fitting relaxation times with Arrhenius models and extracting activation energies, the study quantified how structural features regulate energy dissipation. Further, their 'materials genome sequencing' framework linked functional group type, defect configuration, and conductive network connectivity to electromagnetic response (Fig. 5c). Subsequent work combined atomic-scale characterization with variable-temperature measurements to construct 3D mappings of frequency, temperature, and polarization, extending visual interpretability of defect-induced responses in realistic 2D systems^[64].

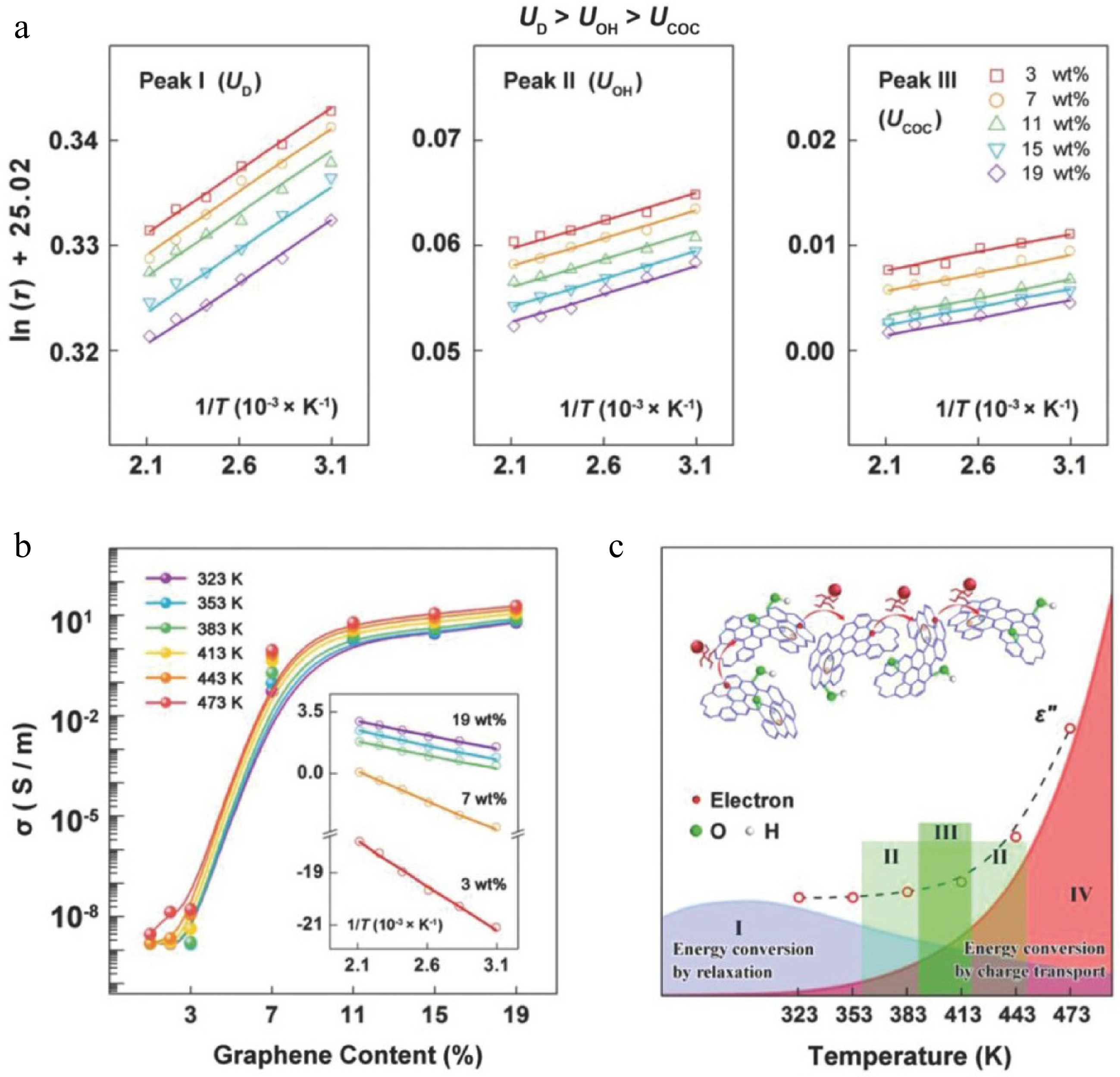
Figure 5. 

(a) Arrhenius plots of ln(τ) vs inverse temperature (T⁻¹) for relaxation peaks of different defect-induced dipoles. (b) Conductivity (σ) as a function of graphene content from 323 to 473 K (inset: ln(σ) vs T⁻¹, where the charge transport barrier is proportional to the absolute slope). (c) Temperature dependence of polarization relaxation loss (ε_p″), and charge transport loss (ε_c"), with regions I−IV indicating: I—dominance of ε_p"; II—synergistic and competitive interaction between ε_p″ and ε_c″; III—equilibrium between ε_p" and ε_c"; IV—dominance of ε_c"^[64].

In heterogeneous hybrid systems, statistical modeling can simultaneously reveal mechanisms and guide parameter optimization. For instance, in CNTs@PANi composites, the degree of CNT oxidation affects dielectric response. By constructing Cole–Cole plots and analyzing loss tangent factors, ε″ was decomposed into ε_p″ and ε_c″, forming a tunable loss mechanism model that guides precise interfacial structural control^[65].

Recently, deep learning models have enhanced the visualization and mechanistic understanding of complex porous nanocomposites. A modified ResNet was trained on SEM image datasets of porous composites for electromagnetic interference shielding^[66]. Eigen-CAM visualization highlighted that pore number and depth critically influence shielding mechanisms, while shallow pores contribute less to EMW absorption (Fig. 5d). By combining DCNN-based visual interpretability with experimental validation, this approach offers a direct and intuitive mapping between microstructural features and shielding performance, complementing traditional statistical inference.

Collectively, these studies demonstrate that statistical methodologies—spanning machine learning, probabilistic modeling, and deep neural networks—have evolved from tools for performance prediction into platforms for mechanistic insight and structural regulation. By constructing interpretable, data-driven causal models, researchers can now synergistically analyze structure, mechanism, and performance, laying a solid foundation for the rational design of next-generation programmable absorbers and multifunctional responsive systems.

Parameter inversion and rapid simulation

The integration of statistical computational theories with numerical simulation methods has emerged as an efficient and reliable strategy for parameter inversion, field distribution modeling, and structural response prediction in electromagnetic functional materials. Compared with traditional trial-and-error experimental workflows, these approaches leverage physics-driven models augmented with probabilistic statistics and optimization algorithms, achieving significant gains in analytical efficiency without compromising prediction accuracy. Such methodologies are particularly advantageous for high-frequency response modeling, complex structural solving, and uncertainty quantification in advanced material systems.

In the domain of frequency-dependent parameter prediction, linear response theory combined with first-principle simulations has been employed to systematically analyze the electromagnetic behavior of ferrite materials in the microwave regime. By mapping electronic structure characteristics to frequency-dependent permittivity and permeability, researchers can predict parameter evolution trends without extensive experimental measurements^[67], providing a computational framework for performance evaluation and material screening. Similarly, Liu & McLeod developed a fast solver based on the discrete dipole approximation (DDA), which models electromagnetic-responsive media as dipole arrays, significantly reducing computational cost while preserving detailed field distributions (Fig. 6a)^[68]. Spatial mapping methods (SMM) further reconstruct electromagnetic responses across multilayer structures, efficiently simulating localized field enhancements in periodic and multiscale architectures without the computational bottlenecks of conventional FDTD approaches^[69].

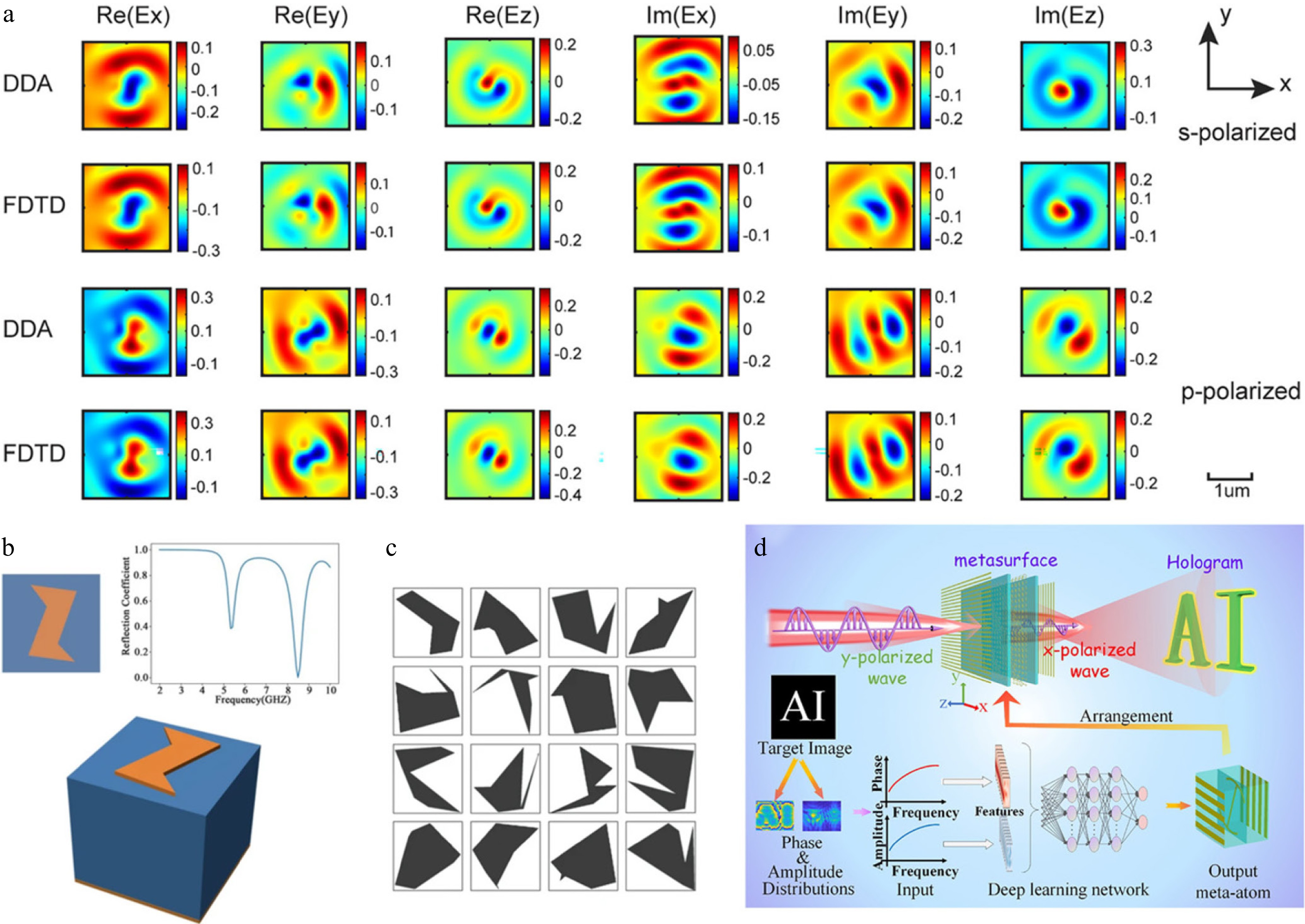
Figure 6. 

(a) Convergence of 1D cylindrical Green's function discrete dipole approximation (DDA) results validated against finite-difference time-domain (FDTD) simulations. Real and imaginary components of the electric field computed by both methods for a larger gold elliptic cylinder at discretization factor D = 3^[68]. (b) A sample of data consisting of a 2D cross-sectional image of a structural design and the corresponding conversion efficiency as an optical response^[71]. (c) Example of a random polygon dataset for CGAN training^[71]. (d) Schematic diagram of the deep learning network empowered metasurface hologram inverse design via the simultaneous control of phase and amplitude^[72].

Statistical uncertainty analysis has also been integrated into electromagnetic parameter inversion. By combining Bayesian error estimation, stochastic Cramér–Rao bounds (sCRB), and minimum uncertainty path (MPU) optimization, these methods robustly identify critical model parameters even with limited or noisy data. Optimal search trajectories within parameter space and dynamic inversion error quantification substantially improve controllability and interpretability, representing a paradigm shift in modeling complex functional materials^[70].

Recent advances in deep learning have further transformed the inverse design of electromagnetic structures, particularly metasurfaces and holographic devices. Xu et al. utilized a conditional generative adversarial network (CGAN) to perform freeform metasurface inverse design, where the generator model maps desired spectral responses to corresponding unit cell geometries and patterns^[71] (Fig. 6b, c). This conditional approach enables rapid design of target electromagnetic responses without iterative parameter scanning. Complementarily, a custom deep ResNet architecture, combining convolutional layers, residual blocks, and fully connected layers, has been employed to realize holographic metasurfaces with simultaneously customized phase and amplitude. By cascading phase and amplitude as 2D input and mapping directly to geometric parameters, the model replaces traditional exhaustive simulation, achieving one-step inverse design of complex amplitude-phase responses^[72] (Fig. 6d). These deep learning frameworks significantly accelerate the design cycle for advanced metasurfaces, providing an intuitive mapping from desired electromagnetic behavior to structural parameters.

Collectively, these strategies demonstrate that integrating statistical modeling, probabilistic inference, and deep learning with physical simulation establishes a closed-loop 'modeling–prediction–inversion–validation' framework. Such approaches not only enhance efficiency and accuracy but also provide rigorous theoretical and computational foundations for tunable material design, rapid performance screening, and synergistic optimization of structural and functional responses in complex electromagnetic systems.

Despite the demonstrated strength of statistical methods in modeling and performance prediction for electromagnetic functional materials, significant challenges and limitations remain. First, model generalizability is often limited, particularly when applied across different material systems or frequency ranges. Many studies rely on models trained under specific experimental conditions without fully capturing the underlying physical principles of the materials, resulting in markedly diminished extrapolation capabilities for novel structures or broader frequency domains. For example, in the design of ultra-broadband terahertz absorbers based on patterned graphene metasurfaces, machine learning models achieved excellent predictive performance within the original metasurface structures and frequency bands; however, their adaptability to other configurations was notably inadequate^[11]. Similarly, another work employing random forest algorithms for rapid prediction of absorption performance in flexible graphene composites demonstrated strong results on the original dataset but relied heavily on fixed experimental parameters, limiting extension to novel composite systems^[55]. These cases highlight a common issue: complex models trained on small samples with high-dimensional features tend to learn 'data representations' rather than 'physical mechanisms', potentially leading to 'high predictive accuracy but poor physical interpretability'.

The field lacks standardized modeling protocols and unified frameworks for multiscale data integration. Divergent practices in feature selection, training–testing splits, and evaluation metrics impede comparability and critical reproducibility of results. For instance, a study integrating crystal graph neural networks with active learning for screening 2D magnetic materials incorporated multi-source data such as structural graphs and electronic density of states; however, the input space employed differs substantially from that used in discrete dipole approximation (DDA) or finite-difference time-domain (FDTD) based structural response simulations, complicating data granularity alignment and cross-method interoperability^[61]. Furthermore, approaches such as spatial mapping methods (SMM) and fast electromagnetic propagation simulations face challenges in synergistically coupling multiscale structural information with modeling variables^[70].

A more pressing issue lies in the limited incorporation of microscopic structural variables in most models. While some studies have attempted to enhance interpretability by integrating factors such as interfacial charge redistribution or defect-induced dipoles—for instance, explaining dielectric loss mechanisms via single-atom configurations and localized charge density variables^[5], or using Cole–Cole analysis to identify multiple Debye relaxation processes and quantify interfacial polarization contributions in hybrid materials^[65]—the majority still rely predominantly on macroscopic input parameters such as volume fraction, thickness, and frequency, neglecting critical microscopic factors like defects, grain boundaries, and functional groups that decisively influence electromagnetic responses. This insufficient dimensionality in characterization hampers the establishment of constitutive mappings among structure, mechanism, and performance, thereby limiting the interpretive depth and physical transferability of statistical models.

The integration of statistical models with fundamental electromagnetic physical laws remains inadequate. Electromagnetic properties are inherently constrained by Maxwell's equations, dispersion relations, and dielectric polarization theories; however, current modeling workflows are predominantly data-driven and lack explicit incorporation of physical priors. To address this limitation, recent advances have explored embedding physical constraints directly into the modeling workflow. Physics-informed neural networks (PINNs) can enforce Maxwell's equations and boundary conditions within the loss function, ensuring predictions respect conservation laws. Symbolic regression or physics-guided regression can generate interpretable expressions linking microstructural descriptors to macroscopic electromagnetic responses. Additionally, input features can be augmented with microscopic and multiscale descriptors—such as local charge distributions, defect types, or functional group densities—providing physical priors that guide learning and improve extrapolation. Regularization techniques and constrained optimization can incorporate energy conservation, symmetry protections, or known dispersion relations, while multi-scale hybrid models can jointly learn from microscopic simulations and macroscopic measurements, bridging data-driven and physics-based approaches. Although recent efforts have begun embedding physics constraints into training processes—such as PINNs^[73] and symbolic regression algorithms^[74,75]—applications in electromagnetic materials research remain nascent. Their effectiveness and scalability in complex wave-absorbing systems have yet to be rigorously validated. Nonetheless, these strategies offer a promising pathway to enhance model interpretability, physical consistency, and generalization across materials and frequency domains.

In summary, key bottlenecks persist for statistical methods in electromagnetic functional materials research, including poor model generalizability, limited structural characterization dimensionality, inconsistent modeling protocols, and weak physical coupling. Future efforts should prioritize embedding physical laws and multiscale descriptors into statistical workflows, standardizing feature engineering, and developing hybrid data–physics models. Such approaches can elevate statistical methods from auxiliary predictive tools to foundational theoretical pillars, enabling mechanistic elucidation, inverse design, and high-fidelity modeling of complex electromagnetic functional materials.

This review systematically synthesizes recent advances in statistical and deep learning methodologies for electromagnetic functional materials, highlighting three primary domains: performance prediction and optimization, microscopic mechanism elucidation, and parameter inversion with rapid field distribution modeling. Machine learning models—including Random Forests, Support Vector Machines, and Gaussian Process Regression—have markedly improved design efficiency, material screening, and prediction accuracy. Deep learning approaches, such as Convolutional Neural Networks, ResNets, Graph Neural Networks, and Generative Adversarial Networks, have further enabled high-precision prediction of broadband absorption, inverse design of metasurfaces, and rapid mapping from structural images to electromagnetic responses. Interpretable modeling strategies provide mechanistic insight, including identification of interfacial effects, defect-induced polarization, and dipole dynamics. Integration with conventional numerical simulations enhances computational efficiency and supports high-fidelity parameter inversion and field modeling.

Despite these advances, key challenges remain, including limited model generalizability, insufficient microstructural characterization, non-standardized workflows, and incomplete incorporation of physical principles. Future efforts should focus on embedding physical priors, establishing cross-scale data fusion frameworks, incorporating deep learning for automated structure–property mapping, and integrating statistical models with experimental and simulation workflows to enable closed-loop, mechanism-guided material design. By combining predictive efficiency with mechanistic understanding, these methodologies are poised to transform electromagnetic materials research from empirical trial-and-error to data-driven, theory-informed paradigms, accelerating the development of high-performance, tunable, and sustainable functional materials.